科目： 来源： 题型：填空题

科目： 来源： 题型：解答题

14．如图，△ABC中，AB=AC，以AC为直径的⊙O交AB于点M，交BC于点N，连接AN，过点C作⊙O的切线，交AB的延长线于点P．
（1）求证：∠BCP=∠BAN；
（2）若BP=3，MN=2，CB=6，求AM的长．

科目： 来源： 题型：解答题

13．如图，点A在x轴正半轴上，点B（4，m）在直线$y=\frac{1}{2}x$上，∠OBA=90°，BE∥x轴，交y轴于点E，C为OB中点，反比例函数$y=\frac{k}{x}$图象的一支经过点C，且与直线BE交于点D．
（1）k=2，直线AB的函数表达式为y=-2x+10；
（2）连结DC并延长，交x轴于点F，连结OD、BF，试判断四边形OFBD的形状并说明理由；
（3）M为直线AB上一点，若△BCM与△BOA相似，写出M点的坐标．

科目： 来源： 题型：填空题

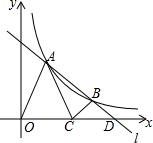12．如图，直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点，l与x轴相交于点D，C为线段OD中点，△OAC与△BCD分别是以OC、CD为底的等腰三角形，且S_△OAC+S_△BCD=2，则k=$\frac{3}{2}$．

科目： 来源： 题型：解答题

11．如图1，在梯形ABCD中，AD∥BC，∠C=90°，点E从点B出发，以某一速度沿折线BA-AD-DC向点C匀速运动；点F从点C出发，以每秒1个单位长的速度向点B匀速运动，点E、F同时出发同时停止．设运动时间为t秒时，△BEF的面积为y，已知y与t的函数关系如图2所示．请根据图中的信息，解答下列问题：
（1）点E运动到A、D两点时，y的值分别是7和4；
（2）求BC和CD的长；
（3）求点E的运动速度；
（4）当t为何值时，△BEF与梯形ABCD的面积之比为1：3？

科目： 来源： 题型：填空题

科目： 来源： 题型：解答题

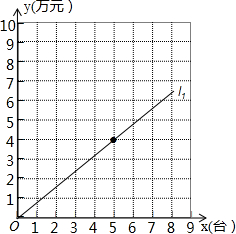9．某专营商场销售一种品牌电脑，每台电脑的进货价是0.4万元．图中的直线l₁表示该品牌电脑一天的销售收入y₁（万元）与销售量x（台）的关系，已知商场每天的房租、水电、工资等固定支出为3万元．
（1）直线l₁对应的函数表达式是y=0.8x，每台电脑的销售价是0.8万元；
（2）写出商场一天的总成本y₂（万元）与销售量x（台）之间的函数表达式：y₂=0.4x+3；
（3）在图的直角坐标系中画出第（2）小题的图象（标上l₂）；
（4）通过计算说明：每天销售量达到多少台时，商场可以盈利．

科目： 来源： 题型：解答题

科目： 来源： 题型：选择题

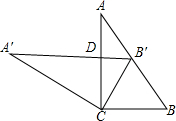7．如图，将两块大小相同的三角板重叠在一起，∠A=30°，∠B=60°，BC=10cm，把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置，点B′在AB上，A′B′与AC相交于点D，则A′D的长度为（　　）

A．

14cm

B．

15cm

C．

16cm

D．

17cm

科目： 来源： 题型：解答题

6．宁波、温州两地相距约300千米，一辆火车和一辆轿车先后从宁波出发去温州，设货车行驶的时间为x（小时），如图线段OA、折线BCD分别表示货车、轿车离宁波距离y（千米）与x（小时）之间的函数关系，根据图象解答下列问题：
（1）货车的行驶速度是60千米/时；轿车到达温州后，货车距离温州30千米．
（2）轿车在行驶过程中进行过一次变速，变速后过多长时间赶上货车？