科目： 来源： 题型：选择题

19．由若干个形状大小相同的小正方体木块组成的几何体的主视图和俯视图如下，则这样的小正方形木块至少有（　　）块．

A．

4

B．

5

C．

6

D．

7

科目： 来源： 题型：解答题

18．已知二次函数图象的顶点坐标为A（2，0），且与y轴交于点（0，1），B点坐标为（2，2），点C为抛物线上一动点，以C为圆心，CB为半径的圆交x轴于M，N两点（M在N的左侧）．
（1）求此二次函数的表达式；
（2）当点C在抛物线上运动时，弦MN的长度是否发生变化？若变化，说明理由；若不发生变化，求出弦MN的长；
（3）当△ABM与△ABN相似时，求出M点的坐标．

科目： 来源： 题型：填空题

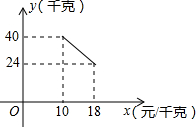17．某经销商销售一种产品，这种产品的成本价为10元/千克，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克，且10≤x≤18）之间的函数关系如图所示，该经销商想要每天获得150元的销售利润，销售价应定为多少？列出关于x方程是（x-10）（-2x+60）=150（不需化简和解方程）．

科目： 来源： 题型：解答题

16．如图1，在平面直角坐标系中，点O为坐标原点，抛物线y=ax²+bx+5与x轴交于点A、点B，与y轴交于点C．直线y=x+2经过点A，交抛物线于点D，AD交y轴于点E，连接CD，CD∥x轴．
（1）求抛物线的解析式；
（2）如图2，过点A的直线交抛物线第四象限于点F，若tan∠BAF=$\frac{1}{2}$，求点F的坐标；
（3）在（2）的条件下，P为直线AF上方抛物线上一点，过点P作PH⊥AF，垂足为H，若HE=PE，求点P的坐标．

科目： 来源： 题型：填空题

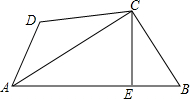15．如图，已知四边形ABCD中，AC平分∠BAD，CE⊥AB于点E，且AE=$\frac{1}{2}$（AB+AD），若∠D=115°，则∠B=65°．

科目： 来源： 题型：解答题

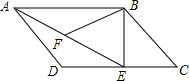14．如图所示，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连接AE，F为AE上一点，且∠BFE=∠C．
（1）求证：△ABF∽△EAD；
（2）若AB=4，∠BAE=30°，AD=3，求AE和BF的长．

科目： 来源： 题型：填空题

13．如图，点P是正方形ABCD的对角线BD上的一点，连接CP并延长，交AD于E，交BA的延长线于点F．若PE=4，EF=5，则线段PC的长为6．

科目： 来源： 题型：解答题

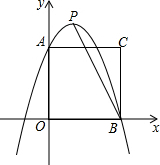12．如图所示，将一边长为3的正方形放置到平面直角坐标系中，其顶点A、B均落在坐标轴上，一抛物线过点A、B，且顶点为P（1，4）
（1）求抛物线的解析式；
（2）点M为抛物线上一点，恰使△MOA≌△MOB，求点M的坐标；
（3）y轴上是否存在一点N，恰好使得△PNB为直角三角形？若存在，直接写出满足条件的所有点N的坐标；若不存在，请说明理由．

科目： 来源： 题型：解答题

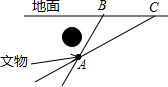11．如图所示，某古代文物被探明埋于地下的A处，由于点A上方有一些管道，考古人员不能垂直向下挖掘，他们被允许从B处或C处挖掘，从B处挖掘时，最短路线BA与地面所成的锐角是56°，从C处挖掘时，最短路线CA与地面所成的锐角是30°，且BC=20m，若考古人员最终从B处挖掘，求挖掘的最短距离．（参考数据：sin56°=0.83，tan56°≈1.48，$\sqrt{3}$≈1.73，结果保留整数）

科目： 来源： 题型：解答题

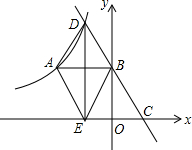10．如图所示，在平面直角坐标系中，双曲线y=$\frac{k}{x}$（x＜0）上有一点A（-2，2），AB⊥y轴于点B，点C是x轴正半轴上一动点，直线CB交双曲线于点D，DE⊥x轴于点E，连接AE，AD，BE．
（1）当点C运动时，四边形ADBE的形状能变成菱形吗？如果能，求出此时点C的位置，若不能，说明理由．
（2）小明经过探究发现：点C运动会影响四边形ADBE形状，但是AD与BE的位置关系始终不变，请你帮他解释其中的原因．