
科目: 来源: 题型:选择题
| A. | 相等的角是对顶角 | |
| B. | 同旁内角相等,两直线平行 | |
| C. | 直线外一点到这条直线的垂线段,叫做点到直线的距离 | |
| D. | 经过直线外一点,有且只有一条直线与这条直线平行 |
查看答案和解析>>
科目: 来源: 题型:选择题
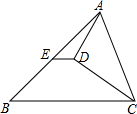 如图,在△ABC中,从A点向∠ACB的角平分线作垂线,垂足为D,E是AB的中点,已知AC=4,BC=6,则DE的长为( )
如图,在△ABC中,从A点向∠ACB的角平分线作垂线,垂足为D,E是AB的中点,已知AC=4,BC=6,则DE的长为( )| A. | 1 | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目: 来源: 题型:选择题
 寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )
寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )| A. | 小明调查了100名同学 | |
| B. | 所得数据的众数是40小时 | |
| C. | 所得数据的中位数是30小时 | |
| D. | 全区有七年级学生6000名,寒假阅读总时间在20小时(含20小时)以上的约有5000名 |
查看答案和解析>>
科目: 来源: 题型:填空题
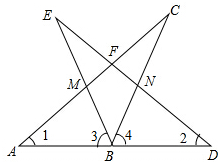 如图,已知△ABC和△BDE,B为AD中点,BE=BC,∠1=∠2,∠3=∠4,请根据题意,写出图中的两对全等三角形:△ABM≌△DBN,△ABC≌△DBE.
如图,已知△ABC和△BDE,B为AD中点,BE=BC,∠1=∠2,∠3=∠4,请根据题意,写出图中的两对全等三角形:△ABM≌△DBN,△ABC≌△DBE.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
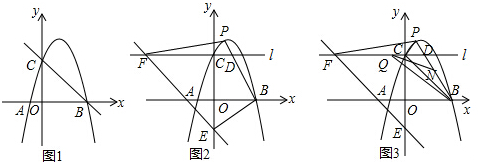
 如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴于D,C两点,连接AC,BC,已知A(0,3),B(4,1).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴于D,C两点,连接AC,BC,已知A(0,3),B(4,1).查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
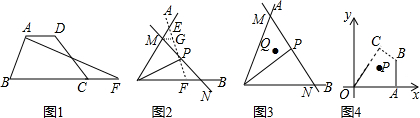
 如图,已知△ABC中,AB=AC.
如图,已知△ABC中,AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com