19．利用一面墙（墙的长度为24m），另三边用用58m长的篱笆围成一个面积为200m²的矩形场地，求矩形的长和宽．

18．活动1：
在一只不透明的口袋中装有标号为1，2，3的3个小球，这些球除标号外都相同，充分搅匀，甲、乙、丙三位同学丙→甲→乙的顺序依次从袋中各摸出一个球（不放回），摸到1号球胜出，计算甲胜出的概率．（注：丙→甲→乙表示丙第一个摸球，甲第二个摸球，乙最后一个摸球）
活动2：
在一只不透明的口袋中装有标号为1，2，3，4的4个小球，这些球除标号外都相同，充分搅匀，请你对甲、乙、丙三名同学规定一个摸球顺序：丙→甲→乙，他们按这个顺序从袋中各摸出一个球（不放回），摸到1号球胜出，则第一个摸球的同学胜出的概率等于$\frac{1}{4}$，最后一个摸球的同学胜出的概率等于$\frac{1}{4}$．
猜想：
在一只不透明的口袋中装有标号为1，2，3，…，n（n为正整数）的n个小球，这些球除标号外都相同，充分搅匀，甲、乙、丙三名同学从袋中各摸出一个球（不放回），摸到1号球胜出，猜想：这三名同学每人胜出的概率之间的大小关系．
你还能得到什么活动经验？（写出一个即可）

17．解下列一元二次方程
①x²-6x+4=0
②2x²-4x+1=0．

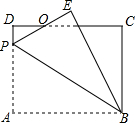16．如图，矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE=OD=1，则AP的长为3.6．

15．今年来某县加大了对教育经费的投入，2013年投入2500万元，2015年投入3500万元．假设该县投入教育经费的年平均增长率为x，根据题意列方程为2500×（1+x）²=3500．

14．一个口袋中有5个黑球和若干个白球，在不允许将球倒出来数的前提下，小明为估计其中的白球数，才用了如下的方法；从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色，不断重复上述过程．小明共摸了100次，其中20次摸到黑球．根据上述数据，小明可估计口袋中的白球大约有20个．

13．某园林门票每张10元，只供一次使用，考虑到人们的不同需求，园林管理处还推出一种“购个人年票”的售票方法（个人年票从购买之日起，可供持票者使用一年）．年票分A、B、C三类：A类年票每张120元，持票者进人园林时无需再购买门票；B类年票每张60元，持票者进入园林时，需再购买门票，每次2元；C类年票每张40元，持票者进入该园林时，需再购买门票，每次3元．
（1）如果你只选择一种购票方式，并且你计划在一年中用80元花在该园林的门票上，试通过计算，从以上4种购票方式中找出进入该园林次数最多的购票方式；
（2）设一年中进园次数为x，分别写出购买B、C两类年票的游客全年的进园购票费用y与x的函数关系；当x≥10时，购买B、C两类年票，哪种进园费用较少？
（3）求一年中进入该园林至少超过多少次时，购买A类门票进园的费用最少．

12．我国宣布划设东海防空识别区如图所示，具体范围为六点连线与我领海线之间空域．其A、B、C三点的坐标数据如表：

	A	B	C
北纬（度）	31°00′	33°11′	25°38′
东经（度）	128°20′	125°00′	125°00′

（1）A点与B或C两点的经度差为$\frac{10}{3}$（单位：度）．
（2）通过测量发现，∠BAC=95°，∠BCA=30°，已知北纬31°00′（即点A所在的纬度）处两条相差1°的经线之间的实际距离为96km．我空军一架巡逻机在该区域执行巡逻任务，飞行速度为30km/min，求飞机沿东经125°经线方向从B点飞往C点大约需要多少时间．（已知tan35°=0.7，tan55°=$\frac{10}{7}$，结果保留整数）

11．已知抛物线C：y=x²-4x+3．
（1）求该抛物线关于y轴对称的抛物线C₁的解析式．
（2）将抛物线C平移至C₂，使其经过点（1，4）．若顶点在x轴上，求C₂的解析式．

10．某班开展安全知识竞赛活动，满分为100分，得分为整数，全班同学的成绩都在60分以上．班长将所有同学的成绩分成四组，并制作了所示的统计图表：

类别	成绩	频数
甲	60≤m＜70	5
乙	70≤m＜80	a
丙	80≤m＜90	10
丁	90≤m≤100	5

根据图表信息，回答下列问题：
（1）该班共有学生40人；表中a=20；
（2）丁组的五名学生中有2名女生，3名男生，现从丁组中随机挑选两名学生参加学校的决赛，请借助树状图、列表或列举等方式，求参加决赛的两名学生是一男、一女的概率．