科目： 来源： 题型：填空题

科目： 来源： 题型：填空题

科目： 来源： 题型：填空题

科目： 来源： 题型：解答题

2．如图，已知抛物线y=ax²+bx+3（a≠0）与x轴交于点A（-1，0），点B（3，0），与y轴交于点C，顶点为D，连接BC．
（1）求抛物线的解析式及顶点D的坐标；
（2）如图1，点E，F为线段BC上的两个动点，且$EF=2\sqrt{2}$，过点E，F作y轴的平行线EM，FN，分别与抛物线交于点M，N，连接MN，设四边形EFNM面积为S，求S的最大值和此时点M的坐标；
（3）如图2，连接BD，点P为BD的中点，点Q是线段BC上的一个动点，连接DQ，PQ，将△DPQ沿PQ翻折得到△D′PQ，当△D′PQ与△BCD重叠部分的面积是△BDQ面积的$\frac{1}{4}$时，求线段CQ的长．

科目： 来源： 题型：解答题

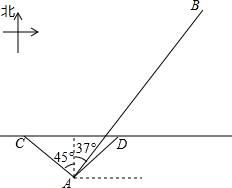1．我国南海某海域有一个固定侦测点A，该侦测点的可侦测半径为$10\sqrt{2}$海里．某天，在点A侦测到西北方向上的点C处有一可疑船恰好进入侦测区域，且往正东方向匀速航行，我方与其进行多次无线电沟通无果后，可疑船只于2小时后恰好在D处离开侦测区域，我方立即通知（通知时间忽略不计）位于点A北偏东37°方向，且与A相距50海里的B处的军舰往正南方向对可疑船只进行侦测拦截．
（1）求可疑船只的速度及点B到直线CD的距离；
（2）若军舰航行速度为20海里/时，可侦测半径为10海里，问军舰最快几小时可以侦测到可疑船只？（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

科目： 来源： 题型：填空题

20．如图，O点在直线AB上，∠AOD=90°，∠COE=90°，则图中相等的锐角有2对．

科目： 来源： 题型：选择题

19．如图，把一块直角三角板的直角顶点放在直尺的一边上，如果∠1=35°，那么∠2是（　　）°．

A．

55

B．

35

C．

65

D．

25

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

17．如图，在平面直角坐标系中，点O为坐标原点，直线y=kx+3与x轴交于点A，与y轴交于点C，过点C的抛物线$y=\frac{1}{2}{x^2}+bx+c$与直线AC交于另一点B，点B坐标为（$\frac{7}{2}$，$\frac{45}{8}$）．
（1）求直线和抛物线的解析式；
（2）点P是射线CB上的一个动点，过点P作直线PQ⊥x轴，垂足为点Q，交抛物线于点D，
①当PD=PC时，求点P的坐标．
②在x轴上点Q的右侧取点M，使MQ=$\frac{3}{2}$，在QP的延长线上取点N，连接PM，AN，已知tan∠NAQ-tan∠MPQ=$\frac{3}{4}$，求线段PN的长．

科目： 来源： 题型：解答题