
科目: 来源: 题型:解答题
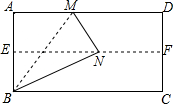 如果是我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法(如图):
如果是我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法(如图):查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:填空题
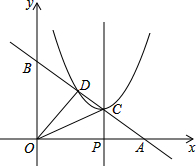 已知直线y=-$\frac{3}{4}x+3$分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒,以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D,设△COD的OC边上的高为h,当t=$\frac{36}{25}$时,h的值最大.
已知直线y=-$\frac{3}{4}x+3$分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒,以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D,设△COD的OC边上的高为h,当t=$\frac{36}{25}$时,h的值最大.查看答案和解析>>
科目: 来源: 题型:解答题
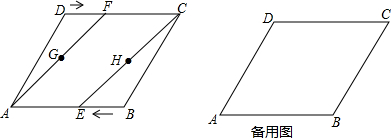
查看答案和解析>>
科目: 来源: 题型:解答题
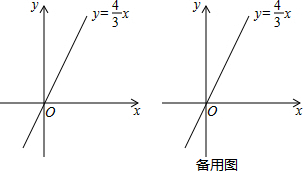
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com