
科目: 来源: 题型:选择题
| A. | 28.09×108 | B. | 2.809×108 | C. | 28.09×109 | D. | 2.809×109 |
查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
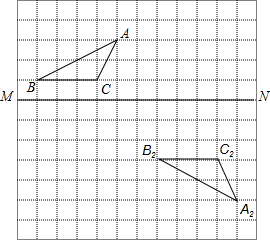 在如图所示的方格纸中.
在如图所示的方格纸中.查看答案和解析>>
科目: 来源: 题型:解答题
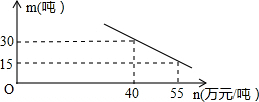 某口生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系:y=-0.5x+50.
某口生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系:y=-0.5x+50.查看答案和解析>>
科目: 来源: 题型:选择题
 如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )| A. | π | B. | 2π | C. | $\frac{π}{2}$ | D. | 4π |
查看答案和解析>>
科目: 来源: 题型:解答题
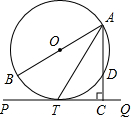 如图,AB为⊙O的直径,PQ切⊙O于T,AC⊥PQ于C,交⊙O于D.
如图,AB为⊙O的直径,PQ切⊙O于T,AC⊥PQ于C,交⊙O于D.查看答案和解析>>
科目: 来源: 题型:解答题
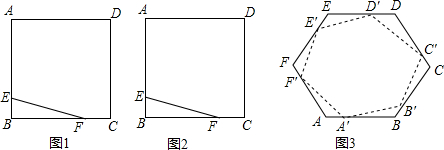
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com