
科目: 来源: 题型:解答题
 已知关于x的一元二次方程x2$+2x+\frac{k-1}{2}=0$有两个不相等的实数根,k为正整数.
已知关于x的一元二次方程x2$+2x+\frac{k-1}{2}=0$有两个不相等的实数根,k为正整数.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
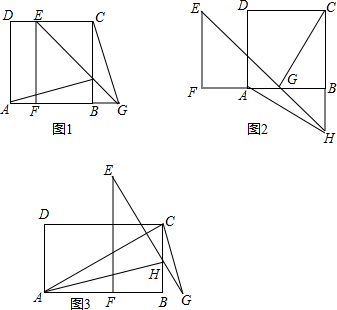
 如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形 ABCD 的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5.
如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形 ABCD 的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5. 查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 在y轴右侧该抛物线上不存在点M,使S△ACM=3 | |
| B. | 在y轴右侧该抛物线上存在两个点M,使S△ACM=3 | |
| C. | 在y轴右侧该抛物线上存在唯一的点M(2,3),使S△ACM=3 | |
| D. | 在y轴右侧该抛物线上存在唯一的点M(2,-3),使S△ACM=3 |
查看答案和解析>>
科目: 来源: 题型:解答题
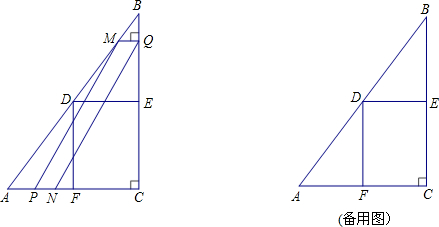
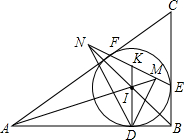 如图,△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,直线EF与直线AI,BI,DI分别相交于点M,N,K.
如图,△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,直线EF与直线AI,BI,DI分别相交于点M,N,K.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com