
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
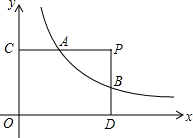 如图,点P(a,b)在第一象限内,PC⊥y轴于点C,PD⊥x轴于点D,两条垂线交反比例函数y=$\frac{k}{x}$的图象于点A、B.
如图,点P(a,b)在第一象限内,PC⊥y轴于点C,PD⊥x轴于点D,两条垂线交反比例函数y=$\frac{k}{x}$的图象于点A、B.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
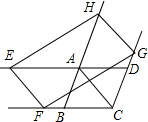 如图,直线EF与?ABCD的对角线AC平行,分别交DA,CB的延长线于点E,F,直线GH与AC平行,分别交CD,BA的延长线于点G,H,则EF与HG的关系是EF=HG,EF∥HG.
如图,直线EF与?ABCD的对角线AC平行,分别交DA,CB的延长线于点E,F,直线GH与AC平行,分别交CD,BA的延长线于点G,H,则EF与HG的关系是EF=HG,EF∥HG.查看答案和解析>>
科目: 来源: 题型:选择题
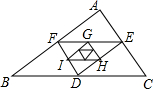 如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | $\frac{1}{{2}^{n+1}}$ | D. | $\frac{1}{{2}^{n+2}}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
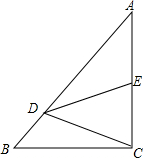 如图,在Rt△ABC中,∠ACB=90°,点D在边AB上,线段DC绕点D按逆时针旋转,端点C恰巧落在边AC上的点E处,已知$\frac{AD}{DB}$=4,求$\frac{AE}{EC}$的值.
如图,在Rt△ABC中,∠ACB=90°,点D在边AB上,线段DC绕点D按逆时针旋转,端点C恰巧落在边AC上的点E处,已知$\frac{AD}{DB}$=4,求$\frac{AE}{EC}$的值.查看答案和解析>>
科目: 来源: 题型:解答题
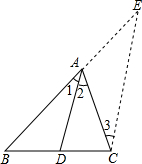 请阅读下面的材料,并回答所提出的问题.
请阅读下面的材料,并回答所提出的问题.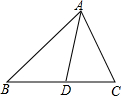
查看答案和解析>>
科目: 来源: 题型:解答题
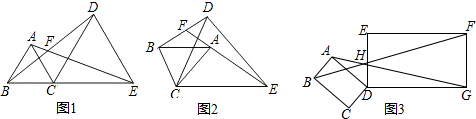
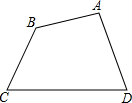 如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?
如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com