15．下列能构成直角三角形的一组数是（　　）

A．

2、3、4

B．

6、8、9

C．

5、12、13

D．

1、1、2

14．（1）计算：（-1）³-（2-5）+$\sqrt{8}$×$\sqrt{2}$；        
（2）化简：$\frac{2x}{{x}^{2}-4}$•$\frac{2x+{x}^{2}}{{x}^{2}}$．

13．如图，若直线a∥b，那么∠x=64度．

12．解方程：
（1）2（3-y）=-4（y+5）；
（2）$\frac{3x-2}{4}$=$\frac{3}{8}$；
（3）$\frac{3x+4}{2}$-$\frac{7-2x}{12}$=1；
（4）x-$\frac{3-2x}{2}$=1-$\frac{x+2}{6}$．

11．（1）问题背景：
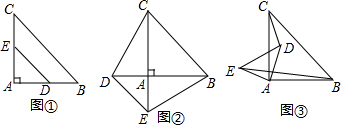
如图（1），在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E，F分别是BC，CD上的点．且∠EAF=60°，探索EF，BE，FD的数量关系，王岩和张放两位同学探索的思路虽然不尽相同，但都得出了正确的结论．
     王岩是这样想的：把△ABE绕着点A逆时针旋转到使AB与AD重合，得△ADG，并确定点F，D，G在一条直线上，再证明△AEF≌AGF…
     张放是这样想的：延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，△AEF≌△AGF…
他们得出的结论是EF=BE+DF．
（2）探索延伸：
如图（2），若在四边形ABCD中，AB=AD，∠B+∠D=180°．E，F分别是BC，CD上的点，且∠EAF=$\frac{1}{2}$∠BAD，（1）中的结论是否仍然成立？并说明理由；
（3）实际应用：
如图（3），在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心（O处）南偏东70°的B处，并且两舰艇到指挥中心的距离都是90海里，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，同时，舰艇乙沿着射线BM的方向（∠OBF=120°），以14海里/小时的速度前进1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且舰艇乙在指挥中心南偏东80°，试问，两舰艇E，F之间的距离是否符合（2）的条件？如果符合，请求出两舰艇之间的距离（画出辅助线）；如果不符合，请说明理由．

10．如图，在Rt△ABC中，∠ACB=90°，$\frac{BC}{AC}$=$\frac{m}{n}$，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F．
（1）探究发现：
如图1，若m=n，点E在线段AC上，则$\frac{DE}{DF}$=1；
（2）数学思考：
①如图2，若点E在线段AC上，则$\frac{DE}{DF}$=$\frac{n}{m}$（用含m，n的代数式表示）；
②当点E在直线AC上运动时，①中的结论是否任然成立？请仅就图3的情形给出证明；
（3）拓展应用：若AC=$\sqrt{5}$，BC=2$\sqrt{5}$，DF=4$\sqrt{2}$，请直接写出CE的长．

9．如图①，在△ABC中，∠A=90°，AB=AC，点D、E分别在AB、AC上，∠ADE=∠ABC．
初步感知：将图①中△ADE绕点A顺时针旋转α度，当α=180°时，如图②，易知△ABE和△ADC的面积相等．（不用证明）
深入探究：将图①中的△ADE绕点A顺时针α度，当0°＜α＜180°时，如图③，猜想△ABE和△ADC的面积之间的关系，并说明理由．
简单应用：将△ADE绕点A顺时针旋转α度，当AB=5，AD=3时，在旋转过程中，△ABE与△ADC面积的和达到的最大值为15．

8．解方程：
（1）3（2x-1）-2（1-x）=-1
（2）$\frac{y-1}{2}$=2-$\frac{y+2}{5}$．

7．关于x的方程mx+4=3x+5的解是x=-1，则m=2．

6．如图，点F、C在BE上，BF=CE，∠A=∠D，∠B=∠E．
求证：AB=DE．