
科目: 来源: 题型:选择题
 如图,在平面直角坐标系中,若有一点P(2,1)向上平移3个单位或者向左平移4个单位,恰好在直线y=kx+b上,则k的值是( )
如图,在平面直角坐标系中,若有一点P(2,1)向上平移3个单位或者向左平移4个单位,恰好在直线y=kx+b上,则k的值是( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 了解某班同学的体重情况 | B. | 了解我省初中学生的兴趣爱好情况 | ||
| C. | 了解一批电灯泡的使用寿命 | D. | 了解我省农民工的年收入情况 |
查看答案和解析>>
科目: 来源: 题型:解答题
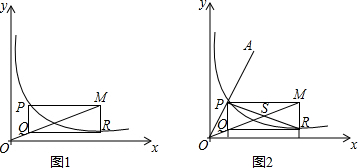
查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
 在平面直角坐标系中,二次函数y=x2+mx+2m-7的图象经过点(1,0).
在平面直角坐标系中,二次函数y=x2+mx+2m-7的图象经过点(1,0).查看答案和解析>>
科目: 来源: 题型:填空题

查看答案和解析>>
科目: 来源: 题型:解答题
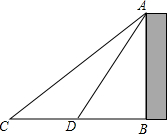 天津北宁公园内的致远塔,塔高九层,塔内四周墙壁上镶钳着历史题材为内容的瓷板油彩画或青石刻浮雕,叠双向盘旋楼梯或电梯可达九层,津门美景尽收眼底,是我国目前最高的宝塔.某校数学情趣小组实地测量了致远塔的高度AB,如图,在C处测得塔尖A的仰角为45°,再沿CB方向前进31.45m到达D处,测得塔尖A的仰角为60°,求塔高AB(精确到0.1m,$\sqrt{3}$≈1.732)
天津北宁公园内的致远塔,塔高九层,塔内四周墙壁上镶钳着历史题材为内容的瓷板油彩画或青石刻浮雕,叠双向盘旋楼梯或电梯可达九层,津门美景尽收眼底,是我国目前最高的宝塔.某校数学情趣小组实地测量了致远塔的高度AB,如图,在C处测得塔尖A的仰角为45°,再沿CB方向前进31.45m到达D处,测得塔尖A的仰角为60°,求塔高AB(精确到0.1m,$\sqrt{3}$≈1.732)查看答案和解析>>
科目: 来源: 题型:解答题
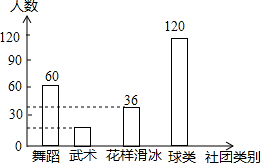 某校开展社团活动,准备组件舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球).花样滑冰四类社团,为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制以下的统计图表,请根据图表中的信息解答下列问题:
某校开展社团活动,准备组件舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球).花样滑冰四类社团,为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制以下的统计图表,请根据图表中的信息解答下列问题:| 社团类别 | 人数 | 占总人数的比例 |
| 舞蹈 | 60 | 25% |
| 武术 | m | 10% |
| 花样滑冰 | 36 | n% |
| 球类 | 120 | 50% |
查看答案和解析>>
科目: 来源: 题型:解答题
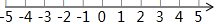
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com