
科目: 来源: 题型:选择题
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
查看答案和解析>>
科目: 来源: 题型:解答题
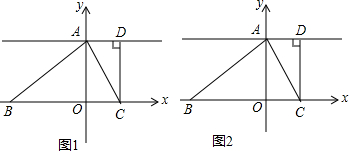
查看答案和解析>>
科目: 来源: 题型:选择题
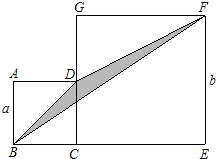 四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为a,正方形CEFG的边长为b,连接BD,BF和DF后得到三角形BDF,请用含字母a和b的代数式表示三角形BDF的面积可表示为( )
四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为a,正方形CEFG的边长为b,连接BD,BF和DF后得到三角形BDF,请用含字母a和b的代数式表示三角形BDF的面积可表示为( )| A. | ab | B. | $\frac{1}{2}$ab | C. | $\frac{1}{2}$b2 | D. | $\frac{1}{2}$a2 |
查看答案和解析>>
科目: 来源: 题型:解答题
 一辆动车从重庆开往成都,一辆高铁从成都开往重庆,两车同时出发,设动车离重庆的距离为y1(cm),高铁离重庆的距离为y2(km),动车行驶时间为t(h),变量y1,y2与t之间的关系图象如图所示:
一辆动车从重庆开往成都,一辆高铁从成都开往重庆,两车同时出发,设动车离重庆的距离为y1(cm),高铁离重庆的距离为y2(km),动车行驶时间为t(h),变量y1,y2与t之间的关系图象如图所示:查看答案和解析>>
科目: 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目: 来源: 题型:填空题
 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:查看答案和解析>>
科目: 来源: 题型:解答题
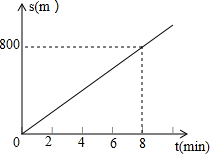 小灰灰和灰太狼一起进行晨练,小灰灰从狼堡先跑8分钟后,灰太狼才从同一起点沿同一路线开始跑,它们的速度一直保持不变,经过2分钟后两人相遇,小灰灰跑过的路程s和所用的时间t之间的关系如图所示,根据图象回答下列问题:
小灰灰和灰太狼一起进行晨练,小灰灰从狼堡先跑8分钟后,灰太狼才从同一起点沿同一路线开始跑,它们的速度一直保持不变,经过2分钟后两人相遇,小灰灰跑过的路程s和所用的时间t之间的关系如图所示,根据图象回答下列问题:查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com