
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
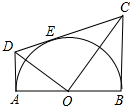 如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )
如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
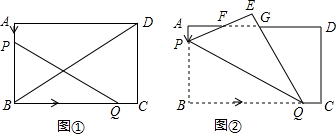 如图①,已知矩形ABCD中,AB=60cm,BC=90cm.点P从点A出发,以3cm/s的速度沿AB运动:同时,点Q从点B出发,以20cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动的时间为t(s).
如图①,已知矩形ABCD中,AB=60cm,BC=90cm.点P从点A出发,以3cm/s的速度沿AB运动:同时,点Q从点B出发,以20cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动的时间为t(s).查看答案和解析>>
科目: 来源: 题型:解答题
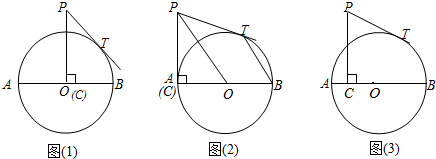
查看答案和解析>>
科目: 来源: 题型:解答题
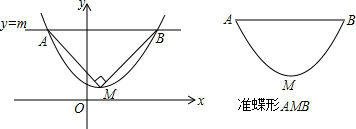
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.
如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.查看答案和解析>>
科目: 来源: 题型:解答题
 已知,如图,抛物线y=-x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα-tanβ=2,OC2=OA•OB.
已知,如图,抛物线y=-x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα-tanβ=2,OC2=OA•OB.查看答案和解析>>
科目: 来源: 题型:解答题
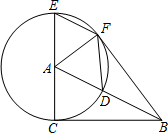 如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.
如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.查看答案和解析>>
科目: 来源: 题型:填空题
 如图所示,分别以Rt△ABC的直角边AC,斜边AB为边向△ABC外构造等边△ACD和等边△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.有下列四个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④$\frac{{S}_{△ACD}}{{S}_{四边形BCDE}}$=$\frac{1}{6}$.其中正确的结论是①②(填写正确结论的序号).
如图所示,分别以Rt△ABC的直角边AC,斜边AB为边向△ABC外构造等边△ACD和等边△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.有下列四个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④$\frac{{S}_{△ACD}}{{S}_{四边形BCDE}}$=$\frac{1}{6}$.其中正确的结论是①②(填写正确结论的序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com