6.阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值.如对于任意正实数a、x,可作变形:x+$\frac{a}{x}$=($\sqrt{x}$-$\frac{\sqrt{a}}{\sqrt{x}}$)2+2$\sqrt{a}$,因为($\sqrt{x}$-$\frac{\sqrt{a}}{\sqrt{x}}$)2≥0,所以x+$\frac{a}{x}$≥2$\sqrt{a}$(当x=$\sqrt{a}$时取等号).
记函数y=x+$\frac{a}{x}$(a>0,x>0),由上述结论可知:当x=$\sqrt{a}$时,该函数有最小值为2$\sqrt{a}$.
直接应用:已知函数y1=x(x>0)与函数y2=$\frac{9}{x}$(x>0),则当x=3 时,y1+y2取得最小值为6.
变形应用:已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),求$\frac{{y}_{2}}{{y}_{1}}$的最小值,并指出取得该最小值时相应的x的值.
实际应用:汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油($\frac{1}{18}$+$\frac{450}{{x}^{2}}$)升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
①求y关于x的函数关系式(写出自变量x的取值范围);
②求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).

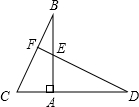 如图,已知Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转,使点D落在射线CA上,DE的延长线交BC于F,则∠CFD的度数为( )
如图,已知Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转,使点D落在射线CA上,DE的延长线交BC于F,则∠CFD的度数为( )