
科目: 来源: 题型:选择题
| A. | 3,1 | B. | 3,-1 | C. | -3,1 | D. | -3,-1 |
查看答案和解析>>
科目: 来源: 题型:解答题
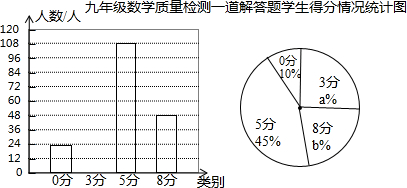
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
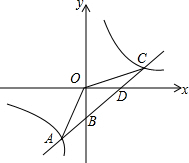 如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.查看答案和解析>>
科目: 来源: 题型:解答题
 如图所示,港口A位于灯场C的正南方向,港口B位于灯场C的南偏东60°方向,且港口B在港口A的正东方向的90海里处.一艘货轮在上午8时从港口A出发,匀速向港口B航行.当航行到位于灯场C的南偏东30°方向的D处时,接到公司要求提前交货的通知,于是提速到原来速度的1.2倍,于上午12时准时列达港口B,顺利完成交货,求货轮原来的速度是多少?
如图所示,港口A位于灯场C的正南方向,港口B位于灯场C的南偏东60°方向,且港口B在港口A的正东方向的90海里处.一艘货轮在上午8时从港口A出发,匀速向港口B航行.当航行到位于灯场C的南偏东30°方向的D处时,接到公司要求提前交货的通知,于是提速到原来速度的1.2倍,于上午12时准时列达港口B,顺利完成交货,求货轮原来的速度是多少?查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com