科目： 来源： 题型：选择题

3．下列几何体中，主视图是圆的是（　　）

A．

圆柱

B．

圆锥

C．

球

D．

立方体

科目： 来源： 题型：选择题

2．在⊙O中，AB是⊙O的直径，AB=8cm，$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$，M是AB上一动点，CM+DM的最小值是（　　）

A．

6cm

B．

8cm

C．

10cm

D．

12cm

科目： 来源： 题型：解答题

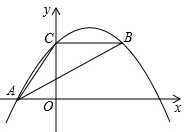1．如图，抛物线y=ax²-4ax+2经过△ABC的三个顶点，已知BC∥x轴，点A在x轴上，点C在y轴上，且OA=OC．
（1）求抛物线的对称轴；
（2）写出A，B，C三点的坐标并出求抛物线的解析式；
（3）探究：若点P是抛物线对称轴上且在x轴下方的动点，是否存在△PAB是等腰三角形．若存在，直接写出所有符合条件的点P坐标；若不存在，请说明理由．

科目： 来源： 题型：解答题

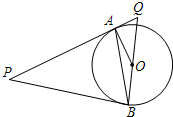20．如图所示．P是⊙O外一点．PA是⊙O的切线．A是切点．B是⊙O上一点．且PA=PB，连接AO、BO、AB，并延长BO与切线PA相交于点Q．
（1）求证：PB是⊙O的切线；
（2）求证：AQ•PQ=OQ•BQ；
（3）设∠AOQ=α，若cosα=$\frac{4}{5}$，OQ=10，求BP的长．

科目： 来源： 题型：解答题

19．如图，把矩形纸片ABCD沿EF折叠，使点B落在边AD上的点B′处，点A落在点A′处．
（1）求证：B′E=BF；
（2）若AE=3，AB=4，求BF的长．

科目： 来源： 题型：选择题

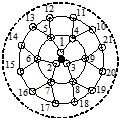18．课题研究小组对附着在物体表面的三个微生物（课题小组成员把他们分别标号为1，2，3）的生长情况进行观察记录．这三个微生物第一天各自一分为二，产生新的微生物（分别被标号为4，5，6，7，8，9），接下去每天都按照这样的规律变化，即每个微生物一分为二，形成新的微生物（课题组成员用如图所示的图形进行形象的记录）．那么标号为150的微生物会出现在（　　）

A．

第3天

B．

第4天

C．

第5天

D．

第6天

科目： 来源： 题型：选择题

科目： 来源： 题型：选择题

科目： 来源： 题型：选择题

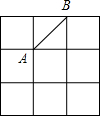15．在边长为2的小正方形组成的网格中，有如图所示的A，B两点，在格点上任意放置点C，恰好能使得△ABC的面积为2的概率为（　　）

A．

$\frac{3}{16}$

B．

$\frac{3}{8}$

C．

$\frac{1}{4}$

D．

$\frac{5}{16}$

科目： 来源： 题型：解答题