
科目: 来源: 题型:解答题
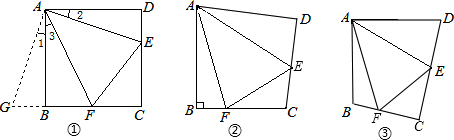
 先阅读材料,解答下列问题:
先阅读材料,解答下列问题:查看答案和解析>>
科目: 来源: 题型:解答题
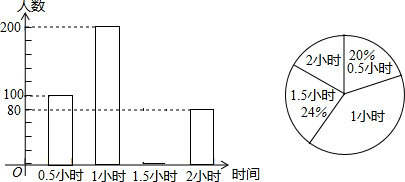
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
 如图,在Rt△ABC中,∠ACB=90°,AC=$\sqrt{3}$,BC=1,以B为圆心,BC长为半径作弧,交AB于点D,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$(结果保留π)
如图,在Rt△ABC中,∠ACB=90°,AC=$\sqrt{3}$,BC=1,以B为圆心,BC长为半径作弧,交AB于点D,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$(结果保留π)查看答案和解析>>
科目: 来源: 题型:解答题
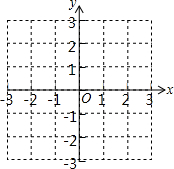 我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1-x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|称为Pl,P2两点间的直角距离,记作d(P1,P2),即d(P1,P2)=|x1-x2|+|y1-y2|.
我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1-x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|称为Pl,P2两点间的直角距离,记作d(P1,P2),即d(P1,P2)=|x1-x2|+|y1-y2|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com