10．如图1，在平面直角坐标系中，抛物线y=-$\frac{1}{3}$x²+$\frac{2\sqrt{3}}{3}$x+3与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，抛物线的顶点为点E．
（1）判断△ABC的形状，并说明理由；
（2）经过B，C两点的直线交抛物线的对称轴于点D，点P为直线BC上方抛物线上的一动点，当△PCD的面积最大时，Q从点P出发，先沿适当的路径运动到抛物线的对称轴上点M处，再沿垂直于抛物线对称轴的方向运动到y轴上的点N处，最后沿适当的路径运动到点A处停止．当点Q的运动路径最短时，求点N的坐标及点Q经过的最短路径的长；
（3）如图2，平移抛物线，使抛物线的顶点E在射线AE上移动，点E平移后的对应点为点E′，点A的对应点为点A′，将△AOC绕点O顺时针旋转至△A₁OC₁的位置，点A，C的对应点分别为点A₁，C₁，且点A₁恰好落在AC上，连接C₁A′，C₁E′，△A′C₁E′是否能为等腰三角形？若能，请求出所有符合条件的点E′的坐标；若不能，请说明理由．

9．从-3，-1，$\frac{1}{2}$，1，3这五个数中，随机抽取一个数，记为a，若数a使关于x的不等式组$\left\{\begin{array}{l}{\frac{1}{3}（2x+7）≥3}\\{x-a＜0}\end{array}\right.$无解，且使关于x的分式方程$\frac{x}{x-3}$-$\frac{a-2}{3-x}$=-1有整数解，那么这5个数中所有满足条件的a的值之和是（　　）

A．

-3

B．

-2

C．

-$\frac{3}{2}$

D．

$\frac{1}{2}$

8．已知点P（x₀，y₀）和直线y=kx+b，则点P到直线y=kx+b的距离证明可用公式d=$\frac{|k{x}_{0}-{y}_{0}+b|}{\sqrt{1+{k}^{2}}}$计算．
例如：求点P（-1，2）到直线y=3x+7的距离．
解：因为直线y=3x+7，其中k=3，b=7．
所以点P（-1，2）到直线y=3x+7的距离为：d=$\frac{|k{x}_{0}-{y}_{0}+b|}{\sqrt{1+{k}^{2}}}$=$\frac{|3×（-1）-2+7|}{\sqrt{1+{3}^{2}}}$=$\frac{2}{\sqrt{10}}$=$\frac{\sqrt{10}}{5}$．
根据以上材料，解答下列问题：
（1）求点P（1，-1）到直线y=x-1的距离；
（2）已知⊙Q的圆心Q坐标为（0，5），半径r为2，判断⊙Q与直线y=$\sqrt{3}$x+9的位置关系并说明理由；
（3）已知直线y=-2x+4与y=-2x-6平行，求这两条直线之间的距离．

7．已知△ABC是等腰直角三角形，∠BAC=90°，CD=$\frac{1}{2}$BC，DE⊥CE，DE=CE，连接AE，点M是AE的中点．
（1）如图1，若点D在BC边上，连接CM，当AB=4时，求CM的长；
（2）如图2，若点D在△ABC的内部，连接BD，点N是BD中点，连接MN，NE，求证：MN⊥AE；
（3）如图3，将图2中的△CDE绕点C逆时针旋转，使∠BCD=30°，连接BD，点N是BD中点，连接MN，探索$\frac{MN}{AC}$的值并直接写出结果．

6．近期猪肉价格不断走高，引起了民众与政府的高度关注．当市场猪肉的平均价格每千克达到一定的单价时，政府将投入储备猪肉以平抑猪肉价格．
（1）从今年年初至5月20日，猪肉价格不断走高，5月20日比年初价格上涨了60%．某市民在今年5月20日购买2.5千克猪肉至少要花100元钱，那么今年年初猪肉的最低价格为每千克多少元？
（2）5月20日，猪肉价格为每千克40元.5月21日，某市决定投入储备猪肉并规定其销售价在每千克40元的基础上下调a%出售．某超市按规定价出售一批储备猪肉，该超市在非储备猪肉的价格仍为每千克40元的情况下，该天的两种猪肉总销量比5月20日增加了a%，且储备猪肉的销量占总销量的$\frac{3}{4}$，两种猪肉销售的总金额比5月20日提高了$\frac{1}{10}$a%，求a的值．

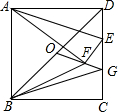5．如图，在正方形ABCD中，AB=6，点E在边CD上，DE=$\frac{1}{3}$DC，连接AE，将△ADE沿AE翻折，点D落在点F处，点O是对角线BD的中点，连接OF并延长OF交CD于点G，连接BF，BG，则△BFG的周长是$\frac{12}{5}$（$\sqrt{5}$+$\sqrt{10}$）．

4．已知a=（-$\frac{1}{2.78}$）⁶⁷，b=（-$\frac{1}{2.78}$）⁶⁸，c=（-$\frac{1}{2.78}$）⁶⁹，判断a、b、c三数的大小关系为下列何者？（　　）

A．

a＞b＞c

B．

b＞a＞c

C．

b＞c＞a

D．

c＞b＞a

3．计算（2x²-4）（2x-1-$\frac{3}{2}$x）的结果，与下列哪一个式子相同？（　　）

A．

-x2+2

B．

x3+4

C．

x3-4x+4

D．

x3-2x2-2x+4

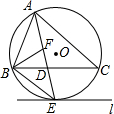2．如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC于点D，过点E做直线l∥BC．
（1）判断直线l与⊙O的位置关系，并说明理由；
（2）若∠ABC的平分线BF交AD于点F，求证：BE=EF；
（3）在（2）的条件下，若DE=4，DF=3，求AF的长．

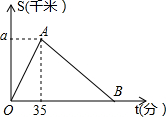1．2016年3月27日“丽水半程马拉松竞赛”在莲都举行，某运动员从起点万地广场西门出发，途经紫金大桥，沿比赛路线跑回终点万地广场西门．设该运动员离开起点的路程S（千米）与跑步时间t（分钟）之间的函数关系如图所示，其中从起点到紫金大桥的平均速度是0.3千米/分，用时35分钟，根据图象提供的信息，解答下列问题：
（1）求图中a的值；
（2）组委会在距离起点2.1千米处设立一个拍摄点C，该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟．
①求AB所在直线的函数解析式；
②该运动员跑完赛程用时多少分钟？