
科目: 来源: 题型:解答题
 抛物线y=ax2-2ax-3a与x轴交于A、B两点(其中A在左侧,B在右侧,且经过点C(2,3).
抛物线y=ax2-2ax-3a与x轴交于A、B两点(其中A在左侧,B在右侧,且经过点C(2,3).查看答案和解析>>
科目: 来源: 题型:解答题
 如图,⊙O1和⊙O2是外切于点P的两个等圆,点A、B分别在⊙O1、⊙O2上,∠APB=90°,和⊙O1、⊙O2的另一个交点分别是C、D.求证:CD=O1O2.
如图,⊙O1和⊙O2是外切于点P的两个等圆,点A、B分别在⊙O1、⊙O2上,∠APB=90°,和⊙O1、⊙O2的另一个交点分别是C、D.求证:CD=O1O2.查看答案和解析>>
科目: 来源: 题型:解答题
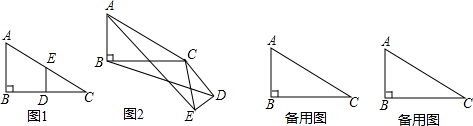
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | “任意选择某一电视频道,它正在播放动画片”是必然事件 | |
| B. | 某运动员投一次篮,投中的概率为0.8,则该运动员投5次篮,一定有4次投中 | |
| C. | 任总抛掷一枚均匀的硬币,反面朝上的概率为$\frac{1}{2}$ | |
| D. | 布袋里有3个白球,1个黑球.任意取出1个球,恰好是黑球的概率是$\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com