4．钟楼是云南大学的标志性建筑之一，某校教学兴趣小组要测量钟楼的高度，如图，他们在点A处测得钟楼最高点C的仰角为45°，再往钟楼方向前进至点B处测得最高点C的仰角为54°，AB=7m，根据这个兴趣小组测得的数据，计算钟楼的高度CD．（tan36°≈0.73，结果保留整数）．

3．如图，一游人由山脚A沿坡角为30°的山坡AB行走600m，到达一个景点B，再由B沿山坡BC行走200m到达山顶C，若在山顶C处观测到景点B的俯角为45°，则山高CD=300+100$\sqrt{2}$m（结果用根号表示）．

2．若2x^2my³与-5xy²ⁿ是同类项，则|m-n|的值是（　　）

A．

0

B．

1

C．

7

D．

-1

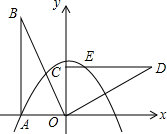1．如图，在平面直角坐标系中，Rt△OAB的直角顶点A在x轴上，顶点B的坐标为（-2，4），抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c经过点A，将Rt△OAB绕着点O按顺时针方向旋转90°得到△OCD，点C为点A的对应点，点E为抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c于线段CD的交点．
（1）用含有b的代数式表示c．
（2）若抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c与△OCD的各边共有两个交点，求b的取值范围．
（3）在图中画出点E旋转前的对应点F，连结OF、EF，设由线段OF、FE、ED、DO首尾顺次连结组成的封闭图形的面积为S．
①当直线EF∥OD时，求线段EF的长．
②当S=6时，求抛物线y=-$\frac{1}{2}$x²+bx+c的表达式．

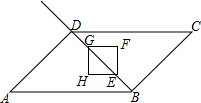20．如图，在平行四边形ABCD中，AB=4$\sqrt{2}$，∠A=45°，∠ADB=90°，点E从点B出发，以每秒1个单位的速度向终点D运动．点G在射线BD上，且EG=2BE（点G在E上方），以EG为对角线作正方形EFGH，设点E的运动时间为t（秒）．
（1）用含t的代数式表示DG的长；
（2）求点H落在AD上时t的值；
（3）设正方形EFGH与平行四边形ABCD的重叠部分图形的面积为S，求S与t之间的函数关系式；
（4）连结FH，直接写出运动过程中线段FH扫过的图形面积．

19．若aⁿ=2，则a³ⁿ的值是8．

18．某市体育协会对2400名年满15岁的男生的身高进行了测量，结果身高（单位：m）在1.68-1.70这一小组的频率为0.25，则该组的人数为（　　）

A．

600人

B．

250人

C．

60人

D．

25人

17．如图，在矩形ABCD中，AD=4，M是AD的中点，点E是线段AB上一动点，连接EM并延长交线段CD的延长线于点F．
感知：如图1，易证：△AEM≌△DFM；（不需要证明）
应用：如图2，若AB=2，过点M作MG⊥EF交线段BC于点G，求证：△GEF是等腰直角三角形；
拓展：如图3，若AB=2$\sqrt{3}$，过点M作MG⊥EF交线段BC的延长线于点G，直接写出$\frac{MG}{ME}$的值．

16．已知5^m=2，5ⁿ=4，求5^2m-n和25^m+n的值．

15．我们可以通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由．

（1）思路梳理
∵AB=AD，
∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．
∵∠ADC=∠B=90°，
∴∠FDG=180°，点F、D、G共线．
根据SAS，易证△AFG≌△AFG，得EF=BE+DF．
（2）类比引申
如图2，四边形ABCD中，AB=AD，∠BAD=90°点E、F分别在边BC、CD上，∠EAF=45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系∠B+∠D=180°时，仍有EF=BE+DF．
（3）联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°．猜想BD、DE、EC应满足的等量关系，并写出推理过程．