
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
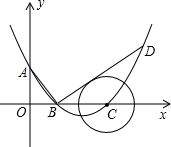 如图,在平面直角坐标系中,抛物线交y轴于A点,交x轴于B(2,0),C(6,0)两点.已知A点坐标为(0,3).
如图,在平面直角坐标系中,抛物线交y轴于A点,交x轴于B(2,0),C(6,0)两点.已知A点坐标为(0,3).查看答案和解析>>
科目: 来源: 题型:选择题
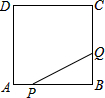 如图,正方形ABCD边长为4,点P从点A运动到点B,速度为1,点Q沿B-C-D运动,速度为2,点P、Q同时出发,则△BPQ的面积y与运动时间t(t≤4)的函数图象是( )
如图,正方形ABCD边长为4,点P从点A运动到点B,速度为1,点Q沿B-C-D运动,速度为2,点P、Q同时出发,则△BPQ的面积y与运动时间t(t≤4)的函数图象是( )| A. |  | B. | 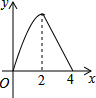 | C. | 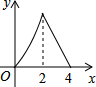 | D. | 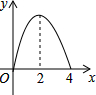 |
查看答案和解析>>
科目: 来源: 题型:填空题
 如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为1或$\frac{\sqrt{3}}{3}$.
如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为1或$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目: 来源: 题型:解答题
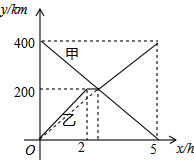 甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:查看答案和解析>>
科目: 来源: 题型:解答题
 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.查看答案和解析>>
科目: 来源: 题型:选择题
| A. | x(a-b)=ax-bx | B. | x2-1+y2=(x-1)(x+1)+y2 | ||
| C. | y2-1=(y+1)(y-1) | D. | ax+by+c=x(a+b)+c |
查看答案和解析>>
科目: 来源: 题型:解答题
 如图所示,BA和CD表示前后两幢楼,按照有感规定两幢楼间的间距不得小于楼的高度,即图中AC大于等于CD,小明想测量一下他家所著AB楼与前面CD楼是否符合规定,于是他在AC间的点M处架了测角仪,测得CD楼顶D的仰角为45°,已知AM=4米,测角仪距地面MN=1.5米.
如图所示,BA和CD表示前后两幢楼,按照有感规定两幢楼间的间距不得小于楼的高度,即图中AC大于等于CD,小明想测量一下他家所著AB楼与前面CD楼是否符合规定,于是他在AC间的点M处架了测角仪,测得CD楼顶D的仰角为45°,已知AM=4米,测角仪距地面MN=1.5米.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com