12．如图，直线a∥b，△ABC为等腰直角三角形，∠BAC=90°，则∠1的度数是（　　）

A．

22.5°

B．

36°

C．

45°

D．

90°

11．已知一次函数y=2x+4
（1）在如图所示的平面直角坐标系中，画出函数的图象；
（2）求图象与x轴的交点A的坐标，与y轴交点B的坐标；
（3）在（2）的条件下，求出△AOB的面积；
（4）利用图象直接写出：当y＜0时，x的取值范围．

10．如图，在Rt△ABC中，∠B=90°，AB=4，BC＞AB，点D在BC上，以AC为对角线的平行四边形ADCE中，DE的最小值是4．

9．将函数y=2x+b（b为常数）的图象位于x轴下方的部分沿x轴翻折至其上方后，所得的折线是函数y=|2x+b|（b为常数）的图象．若该图象在直线y=2下方的点的横坐标x满足0＜x＜3，则b的取值范围为-4≤b≤-2．

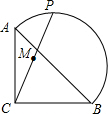8．如图，在等腰Rt△ABC中，AC=BC=2$\sqrt{2}$，点P在以斜边AB为直径的半圆上，M为PC的中点．当点P沿半圆从点A运动至点B时，点M运动的路径长是（　　）

A．

$\sqrt{2}$π

B．

π

C．

2$\sqrt{2}$

D．

2

7．如图，将△ABC绕点A逆时针旋转得到△AB′C′，若B′落到BC边上，∠B=50°，则∠CB′C′的度数为（　　）

A．

50°

B．

60°

C．

70°

D．

80°

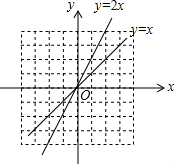6．如图，把函数y=x的图象上各点的纵坐标变为原来的2倍，横坐标不变，得到函数y=2x的图象；也可以把函数y=x的图象上各点的横坐标变为原来的$\frac{1}{2}$倍，纵坐标不变，得到函数y=2x的图象．
类似地，我们可以认识其他函数．
（1）把函数y=$\frac{1}{x}$的图象上各点的纵坐标变为原来的6倍，横坐标不变，得到函数y=$\frac{6}{x}$的图象；也可以把函数y=$\frac{1}{x}$的图象上各点的横坐标变为原来的6倍，纵坐标不变，得到函数y=$\frac{6}{x}$的图象．
（2）已知下列变化：①向下平移2个单位长度；②向右平移1个单位长度；③向右平移$\frac{1}{2}$个单位长度；④纵坐标变为原来的4倍，横坐标不变；⑤横坐标变为原来的$\frac{1}{2}$倍，纵坐标不变；⑥横坐标变为原来的2倍，纵坐标不变．
（Ⅰ）函数y=x²的图象上所有的点经过④→②→①，得到函数y=4（x-1）²-2的图象；
（Ⅱ）为了得到函数y=-$\frac{1}{4}$（x-1）²-2的图象，可以把函数y=-x²的图象上所有的点D．
A．①→⑤→③B．①→⑥→③C．①→②→⑥D．①→③→⑥
（3）函数y=$\frac{1}{x}$的图象可以经过怎样的变化得到函数y=-$\frac{2x+1}{2x+4}$的图象？（写出一种即可）

5．我们在学完“平移、轴对称、旋转”三种图形的变化后，可以进行进一步研究，请根据示例图形，完成下表．

图形的变化	示例图形	与对应线段有关的结论	与对应点有关的结论
平移		（1）AB=A′B′，AB∥A′B′	AA′=BB′ AA′∥BB′
轴对称		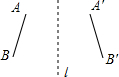（2）AB=A′B′；对应线段AB和A′B′所在的直线如果相交，交点在对称轴l上．	（3）l垂直平分AA′
旋转		AB=A′B′；对应线段AB和A′B′所在的直线相交所成的角与旋转角相等或互补．	（4）OA=OA′，∠AOA′=∠BOB′

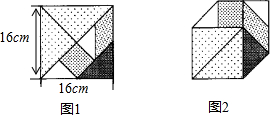4．七巧板是我们祖先的一项卓越创造，被誉为“东方魔板”，小明利用七巧板（如图1所示）中各板块的边长之间的关系拼成一个凸六边形（如图2所示），则该凸六边形的周长是（32$\sqrt{2}$+16）cm．

3．$\sqrt{9}$=（　　）

A．

2

B．

3

C．

4

D．

5