
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
 阅读下列材料:
阅读下列材料:查看答案和解析>>
科目: 来源: 题型:选择题
 如图,点C,E,D在线段AB上,且AB=3AC,AB=4BD,AE=CD.则线段CE与AB长度之间的关系是( )
如图,点C,E,D在线段AB上,且AB=3AC,AB=4BD,AE=CD.则线段CE与AB长度之间的关系是( )| A. | AB=12CE | B. | AB=11CE | C. | AB=10CE | D. | AB=9CE |
查看答案和解析>>
科目: 来源: 题型:填空题
| A品牌(台) | 15 | 17 | 16 | 13 | 14 |
| B品牌(台) | 10 | 14 | 15 | 16 | 20 |
查看答案和解析>>
科目: 来源: 题型:选择题
 二次函数y=-x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
二次函数y=-x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )| A. | t>-5 | B. | -5<t<3 | C. | 3<t≤4 | D. | -5<t≤4 |
查看答案和解析>>
科目: 来源: 题型:解答题
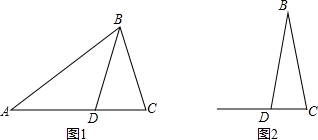 小明在做数学练习时,遇到下面的题目:
小明在做数学练习时,遇到下面的题目: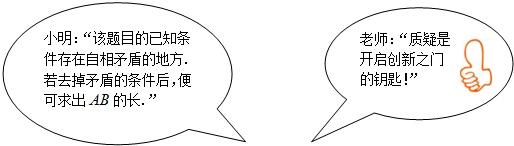
查看答案和解析>>
科目: 来源: 题型:解答题
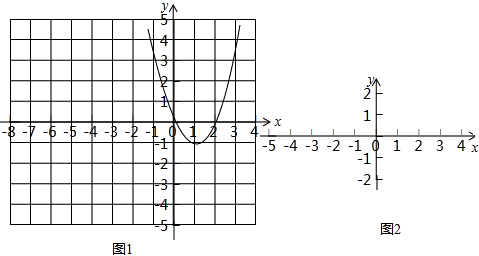 在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$
在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
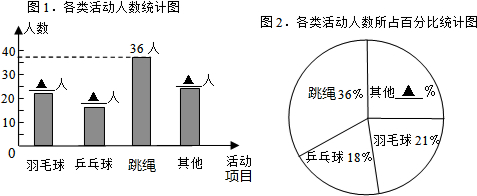
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com