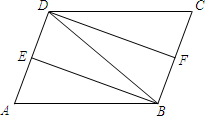7．如图，在?ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．
（1）求证：△ABE≌△CDF；
（2）若AB=DB，求证：四边形DFBE是矩形．

6．在矩形纸片ABCD中，AB=16，AD=12，点P在边AB上，若将△DAP沿DP折叠，使点A恰好落在矩形对角线上的点A′处，则AP的长为6或9．

5．如图，已知抛物线y=ax²-x+c经过点Q （-2，4），且它的顶点P的横坐标为-1．设抛物线与x轴相交于A，B两点，
（1）求抛物线的解析式；
（2）求A，B两点的坐标；
（3）设PB与y轴交于C点，求△ABC的面积．

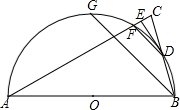4．如图，已知△ABC中，AB=AC，∠A=30°，AB=16，以AB为直径的⊙O与BC边相交于点D，与AC交于点F，过点D作DE⊥AC于点E．
（1）求证：DE是⊙O的切线；
（2）求CE的长；
（3）过点B作BG∥DF，交⊙O于点G，求弧BG的长．

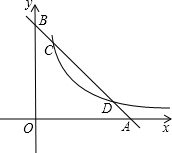3．已知：一次函数y=-x+b的图象与x轴、y轴的交点分别为A、B与反比例函数$y=\frac{5}{x}（x＞0）$的图象交于点C、D，且$\frac{BD}{BA}=\frac{2}{3}$．
（1）求∠BAO的度数；
（2）求O到BC的距离．

2．随着生活水平的提高，人们的健康意识、环保意识都在逐步增强，锻炼形式多种多样，跑步、打拳、徒步、广场舞、球类等等，李叔叔每天上班都坚持骑自行车，如图是他从家出发到单位过程中行进速度v（米/分钟）随时间t（分钟）变化的函数图象大致如图所示，图象由三条线段OA、AB和BC组成．设线段OC上有一动点T（t，0），直线l过点T且与横轴垂直，梯形OABC在直线左侧部分的面积即为t分钟内王叔叔行进的路程s（米）．
（1）当t=2分钟时，速度v=200米/分钟，路程s=200米；
当t=15分钟时，速度v=300米/分钟，路程s=4050米．（直接写出结果即可）．
（2）当0≤t≤3和3＜t≤15时，分别求出路程s（米）关于时间t（分钟）的函数表达式．

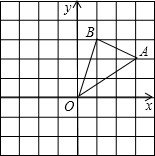1．如图，在边长为1的正方形组成的网格中建立直角坐标系，△AOB的顶点均在格点上，点O为原点，点A，B的坐标分别是（3，2）、B（1，3）．
（1）将△AOB向下平移3个单位后得到△A₁O₁B₁，则点B₁的坐标为（1，0）；
（2）将△AOB绕点O逆时针旋转90°后得到△A₂OB₂，请在图中作出△A₂OB₂，并求出这时点A₂的坐标为（-2，3）；
（3）在（2）中的旋转过程中，线段OA扫过的图形的面积$\frac{\sqrt{13}}{4}$π．

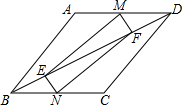20．如图，已知平行四边形ABCD，点M，N分别在边AD和边BC上，点E，F在线段BD上，且AM=CN，DF=BE．求证：
（1）∠DFM=∠BEN；
（2）四边形MENF是平行四边形．

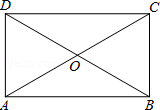19．如图，在?ABCD中，对角线AC，BD相交于点O，且OA=OB．
（1）求证：四边形ABCD是矩形；
（2）若AD=4，∠AOD=50°，求AB的长．（精确到0.1）

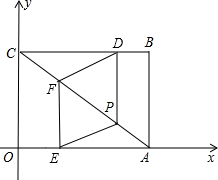18．在直角坐标系中，点O为原点，点B的坐标为（4，3），四边形ABCO是矩形，点D从B出发以每秒1个单位的速度向终点C运动，同时点E从O点出发以每秒1个单位的速度向终点A运动，过D作DP⊥BC与AC交于点P，过E作EF⊥AO与AC交于点F，连结DF、PE．
（1）求出直线AC的解析式，若动点D运动t秒，写出P点的坐标（用含t的代数式表示）；
（2）当t＜2时，四边形EFDP能否是菱形？若能，则求t的值；若不能，请说明理由；
（3）设四边形COEP的面积为S，请写出S与t的函数关系式，并求出S的最小值；
（4）△APE能否是等腰三角形？若能，请直接写出此时P点的坐标．