10．|-$\frac{5}{3}$|的相反数是-$\frac{5}{3}$．

9．如图，在数轴上的点A，B，C，D所表示的数都是整数，若点A与点B的距离是2，点A与点D的距离是3，点D与点C的距离是1，则点B所表示的数是-3．

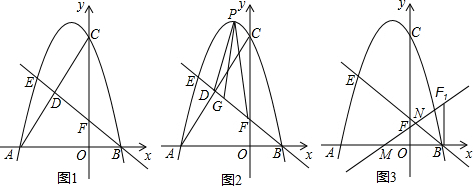
8．如图1，抛物线 y=-$\frac{3}{4}$x²-$\frac{3}{2}$x+6与x轴交于A、B两点（点A在B 的左侧），交y轴交于点C，点D是线段AC的中点，直线BD与抛物线 y=-$\frac{3}{4}$x²-$\frac{3}{2}$x+6交于另一点E，交y轴交于点F．
（1）求直线BE的解析式；
（2）如图2，点P是直线BE上方抛物线上一动点，连接PD、PF，当△PDF的面积最大时，在线段BE上找一点G（不与E、B重合），使得PG-$\frac{3}{5}$GE的值最小，求出点G的坐标及PG-$\frac{3}{5}$GE的最小值；
（3）如图3，将△OBF绕点B顺时针旋转α度（0°＜α＜180°），记旋转过程中的△OBF为△O₁BF₁，直线O₁F₁与x轴交于点M，与直线BE交于点N．在△OBF旋转过程中，是否存在一个合适的位置，使得△MNB是一个等腰三角形？若存在，请直接写出所有符合条件的点N的坐标；若不存在，请说明理由．

7．若一个多边形的内角和是900°，则该多边形至少可被分割为5个三角形．

6．如图，在△ABC中，点O是其重心，连接AO并延长，交BC于点D，则线段AD是△ABC的中线．（填“高”“中线”或“角平分线”）

5．在某三角形中，三边边长均为整数，已知其中一边长为5，若该三角形的周长为20，则其最短一边的边长为5．

4．已知：a是|2|的相反数，b是3的倒数的相反数，c是-3的绝对值，d是$-2\frac{2}{3}$的绝对值，求|a|-|b|-|c|+|d|．

3．如图，有理数a、b、c在数轴上的位置大致如图：

（1）去绝对值符号：|b-c|=b-c，|a-b|=b-a，|a+c|=-a-c
（2）化简：|b-c|-|a-b|-|a+c|．

2．把下列各数分别填入相应的集合里．
-2³，-|-$\frac{4}{3}$|，0，$\frac{22}{7}$，-（-3.14），2006，-（+5），+1.88，
（1）正数集合：{$\frac{22}{7}$，-（-3.14），2006，+1.88…}；
（2）负数集合：{-2³，-|-$\frac{4}{3}$|，-（+5）…}；
（3）整数集合：{-2³，0，2006，-（+5） …}；
（4）分数集合：{-|-$\frac{4}{3}$|，$\frac{22}{7}$，-（-3.14），+1.88 …}．

1．画出如图图形关于直线l的轴对称图形．