18．如图，在△ABC中，∠B=90°，AB=12cm，BC=24cm，动点P从点A开始沿边AB向点B以2cm/s的速度移动，动点Q从点B开始沿变BC向点C以4cm/s的速度移动．如果P，Q两点分别从A，B两点同时出发，求什么时候四边形PQCA的面积为112cm²？

17．如图，Rt△ABC中，∠C=90°，AD平分∠BAC，BD平分∠CBE，AF平分∠DAB，BF平分∠ABD，则∠F=112.5°．

16．在等号成立时，等式右边填上适当的符号：$\frac{y-x}{{{x^2}-{y^2}}}$=-$\frac{1}{x+y}$．

15．如果同位角相等，那么两直线平行（填一个条件满足即可）

14．如图所示，△ABC中，DE∥FG∥BC，且AD=DF=FB，则S_△AFG：S_△ABC=4：9．

13．如果一个三角形的面积扩大9倍，那么它的边长扩大3倍．

12．若（x+y）：y=8：3，则y：x=5：3．

11．已知正方形ABCD的边长为1，AC为对角线，作DO₁⊥AC，O₁为垂足，作O₁O₂⊥AD，O₂为垂足，作O₂O₃⊥AO₁，O₃为垂足，作O₃O₄⊥O₁O₂，O₄为垂足，…，请你仔细观察图，然后计算：$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…=1．

10．问题背景：表是某通讯公司推出的移动电话两种计费方式：

	月使用费/元	主叫限定时间/分	主叫超时费/（元/分）	被叫
方式一	58	150	0.25	免费
方式二	88	350	0.19	免费

若设一个月内用移动电话主叫为t分（t为正整数），根据主叫时间t分析并选择省钱的计费方式．
分析说明：由上表可知，计费与主叫时间相关，计费时首先要看主叫是否超过限定时间．因此，考虑t的取值时，两个主叫限定时间150分和350分是不同时间范围的划分点．
列表解析：当t在不同时间范围内取值时，方式一和方式二的计费如表：（用含t的代数式将表填写完整）

主叫时间t/分	方式一计费/元	方式二计费/元
t小于150	58	88
t=150	58	88
t大于150且小于350	58+0.25（t-150）	88
t=350	108	88
t大于350	108+0.25（t-350）	88+0.19（t-350）

探索比较：由以上分析可知，计费随着主叫时间的变化而变化，比较如下：
①当t小于或等于150分时，因为58＜88，所以按方式一的计费少；
②当t大于150且小于350时，方式一的计费由58元增加到108元，而方式二的计费一直是88元，故可能存在某主叫时间按方式一和方式二的计费相等，请你列方程给予解答说明．
③当t=350时，因为108＞88，所以按方式二的计费较少；
④当t大于350时，由上表可以看出，方式一的计费为108元加上超过350分部分的超时费，方式二的计费为88元加上超过350分部分的超时费，所以按方式二的计费少．
归纳发现：综合上述分析，可以发现：
主叫时间小于270分时，选择方式一省钱；
主叫时间大于270分时，选择方式二省钱．

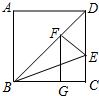9．如图，在矩形ABCD中，已知∠DBC=45°，∠DBC的平分线交DC于点E，作EF⊥BD于点F，作FG⊥BC于点G，则$\frac{BG}{GC}$=$\sqrt{2}$+1．