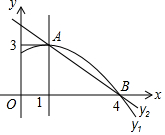17．如图是抛物线y₁=ax²+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y₂=mx+n（m≠0）与抛物线交于A，B两点，下列结论：
①2a-b=0；
②abc＞0；
③方程ax²+bx+c=3有两个相等的实数根；
④抛物线与x轴的另一个交点是（-1，0）；
⑤当1＜x＜4时，有y₂＜y₁，
其中正确的序号是③④⑤．

16．要使关于x的一元二次方程ax²+2x-1=0有两个实数根，且使关于x的分式方程$\frac{x}{x-4}$+$\frac{a+2}{4-x}$=2的解为非负数的所有整数a的个数为（　　）

A．

5个

B．

6个

C．

7个

D．

8个

15．下列调查中，更适合采用普查方式的是（　　）

	A．	调查收看里约奥运会女排决赛的人数
	B．	调查某种灯泡的使用寿命
	C．	调查东台市居民对“中国梦”的知晓率
	D．	调查“天宫二号”零件的质量情况

14．下列方程中是关于x的一元二次方程的是（　　）

A．

x2+2x=x2-1

B．

x3+2x2+3=0

C．

x（x-1）=1

D．

3x2-2xy-5y2=0

13．解方程：$\frac{x+667}{2007}$=$\frac{x+1338}{2010}$-$\frac{669+x}{2013}$．

12．设a、b为有理数，且|a|＞0，方程||x-a|+b|=4有两个不相等的解，求b的值．

11．下列分式是否是最简分式？如果不是，请化简为最简分式
（1）$\frac{2xy}{4xyz}$
（2）$\frac{2ab（a+b）}{（a+b）^{2}}$
（3）$\frac{-（2-x）^{2}}{-（y-2）（x-2）}$
（4）$\frac{m-2n}{{m}^{2}-4mn+4{n}^{2}}$
（5）$\frac{6{x}^{2}-12xy+6{y}^{2}}{3x-3y}$
（6）$\frac{2x-y}{{y}^{2}-4{x}^{2}}$．

10．把下列各式约分：

（1）$\frac{{a}^{2}-ab}{a-b}$	（2）$\frac{2{x}^{4}-4{x}^{3}}{x-2}$	（3）$\frac{{x}^{2}-25}{{x}^{2}-5x}$
（4）$\frac{-（2-x）}{-（y-2）（x-2）}$	（5）$\frac{{x}^{2}+6x+9}{{x}^{2}-9}$	（6）$\frac{{m}^{2}-8m+16}{{m}^{2}-4m}$

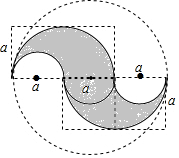9．如图所示是小动动同学设计的“八卦”图形，用字母a表示阴影部分的面积为（　　）

A．

2πa2

B．

（2π-1）a2

C．

πa2

D．

$\frac{3}{4}$πa2

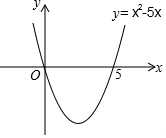8．自主学习，请阅读下列解题过程．
解一元二次不等式：x²-5x＞0．
解：设x²-5x=0，解得：x₁=0，x₂=5，则抛物线y=x²-5x与x轴的交点坐标为（0，0）和（5，0）．画出二次函数y=x²-5x的大致图象（如图所示），由图象可知：当x＜0，或x＞5时函数图象位于x轴上方，此时y＞0，即x²-5x＞0，所以，一元二次不等式x²-5x＞0的解集为：x＜0或x＞5．
通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：
（1）上述解题过程中，渗透了下列数学思想中的①和③．（只填序号）
①转化思想     ②分类讨论思想    ③数形结合思想
（2）一元二次不等式x²-5x＜0的解集为0＜x＜5．
（3）用类似的方法写出一元二次不等式的解集：x²-2x-3＞0．x＜-1或x＞3．