
科目: 来源: 题型:填空题
 一段抛物线:y=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$(0≤x≤3)记为C1,它与x轴交于点O,A1:将C1绕点A1旋转180°得到C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C13,若P(37,m)在第13段抛物线C13上,则m=2.
一段抛物线:y=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$(0≤x≤3)记为C1,它与x轴交于点O,A1:将C1绕点A1旋转180°得到C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C13,若P(37,m)在第13段抛物线C13上,则m=2.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | m=$\frac{1}{2}$n | B. | m=$\frac{1}{4}$n | C. | m=$\frac{1}{2}$n2 | D. | m=$\frac{1}{4}$n2 |
查看答案和解析>>
科目: 来源: 题型:解答题
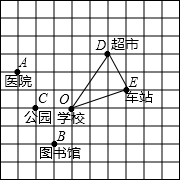 如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题:
如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题:查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com