7．计算
（1）-1⁴-〔2-（-3²）〕÷（-$\frac{1}{2}$）³
（2）-5²-〔2³+﹙1-0.8×$\frac{3}{4}$）÷（-2²）〕
（3）（-$\frac{1}{30}$）÷（$\frac{2}{3}$-$\frac{1}{10}$+$\frac{1}{6}$-$\frac{2}{5}$）
（4）-1²⁰¹⁰÷（-5）²×（-$\frac{5}{3}$）+|0.8-1|
（5）-$\frac{2x-1}{3}$-2（1-x+$\frac{x+1}{2}$）+1．

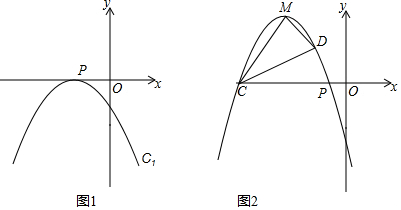6．已知，抛物线C₁：y=-$\frac{1}{2}$x²+mx+m+$\frac{1}{2}$．
（1）①无论m取何值，抛物线经过定点P（-1，0）；
②随着m的取值的变化，顶点M（x，y）随之变化，y是x的函数，则函数C₂的关系式为：y=$\frac{1}{2}$（x+1）²；
（2）如图1，抛物线C₁与x轴仅有一个公共点，请在图1画出顶点M满足的函数C₂的大致图象，平行于y轴的直线l分别交C₁、C₂于点A、B，若△PAB为等腰直角三角形，判断直线l满足的条件，并说明理由；
（3）如图2，二次函数的图象C₁的顶点M在第二象限、交x轴于另一点C，抛物线上点M与点P之间一点D的横坐标
为-2，连接PD、CD、CM、DM，若S_△PCD=S_△MCD，求二次函数的解析式．

5．如图，在平面直角坐标系中，直线y=$\frac{3}{4}$x+2m（m＞0）与x轴交于点A，与y轴交于点B，直线y=-mx+n经过点B，与x轴交于点C，∠BAO=2∠OBC
（1）求m的值
（2）动点P从点O出发，以每秒1个单位的速度沿线段OA向点A运动，动点Q从点A出发，以每秒$\frac{5}{4}$个单位的速度沿线段AB向点B运动，P、Q两点同时出发，当其中一个动点到达终点时，另一个动点也停止运动，连接PQ，设运动时间为t（t＞0）当t为何值时，线段PQ的长度最小？并求出这个最小值
（3）在（2）的条件下，以OB为直径作⊙M，问，是否存在某一时刻t，使直线PQ与⊙M相切，若存在，求出此时t的值；若不存在，请说明理由．

4．如图，在长方形ABCD中，AB=CD=8cm，BC=14cm，点P从点B出发，以2cm/秒的速度沿BC向点C运动，设点P的运动时间为t秒：
（1）BP=2tcm．（用t的代数式表示）
（2）当t为何值时，△ABP≌△DCP？
（3）当点P从点B开始运动，同时，点Q从点C出发，以v cm/秒的速度沿CD向点D运动，是否存在这样v的值，使得△ABP与△PQC全等？若存在，请求出v的值；若不存在，请说明理由．

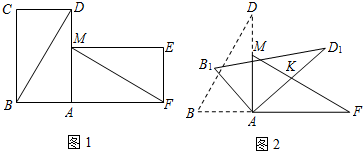
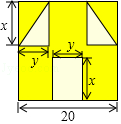3．“囧”（jiong）是近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．
①用含有x、y的代数式表示图中“囧”的面积；
②当x=4，y=$\frac{1}{2}$时，求此时“囧”的面积．

2．有两张完全重合的矩形纸片，小亮将其中一张ABCD绕点A顺时针旋转90°后得到矩形AMEF（如图1），连结BD、MF，此时他测得AF=2cm，∠ADB=30°．
（1）在图1中，直线MF和BD的位置关系为MF⊥BD；
（2）小红同学用剪刀将△BCD与△MEF剪去，与小亮同学继续探究．他们将△ABD绕点A顺时针旋转得△AB₁D₁，AD₁交FM于点K（如图2），设旋转角为β（0°＜β＜90°）
①当△AFK为等腰三角形时，请求出旋转角β的度数；
②请直接写出当△AB₁D₁和△AMF的重叠部分为三角形时旋转角的取值范围，并求出当β=30°时，△AB₁D₁和△AMF重合部分的面积．

1．已知Rt△ABC中，∠C=90°，BC=3，AB=5，那么cos∠B的值是 （　　）

A．

$\frac{3}{5}$

B．

$\frac{3}{4}$

C．

$\frac{4}{5}$

D．

$\frac{4}{3}$

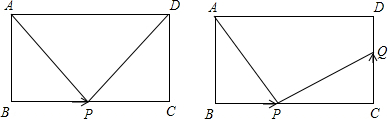
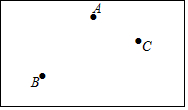20．如图，小明家屋前有一块矩形空地，在空地上的点A、B、C处种有三棵树，小明想在矩形的空地上建一个圆形花坛，使这三棵树都在花坛的边上．
（1）请你帮小明把花坛的位置画出来（用直尺和圆规作图，保留作图痕迹）；
（2）若AB=12m，AC=5m，∠BAC=90°，求小明家花坛的面积（结果保留π）．

19．已知圆锥的底面半径为4cm，母线长为6cm，则它的侧面展开图的面积等于（　　）

A．

24 cm2

B．

48 cm2

C．

24π cm2

D．

12π cm2

18．我国教育事业快速发展，去年普通高校招生人数达5400000人，用科学记数法表示5400000人为 （　　）

A．

5.4×102人

B．

0.54×104人

C．

5.4×106人

D．

5.4×107人