科目： 来源： 题型：解答题

19．已知抛物线G₁：y=a（x-h）²+2的对称轴为x=-1，且经过原点．
（1）求抛物线G₁的表达式；
（2）将抛物线G₁先沿x轴翻折，再向左平移1个单位后，与x轴分别交于A，B两点（点A在点B的左侧），与y轴交于C点，求A点的坐标；
（3）记抛物线在点A，C之间的部分为图象G₂（包含A，C两点），如果直线m：y=kx-2与图象G₂只有一个公共点，请结合函数图象，求直线m与抛物线G₂的对称轴交点的纵坐标t的值或范围．

科目： 来源： 题型：解答题

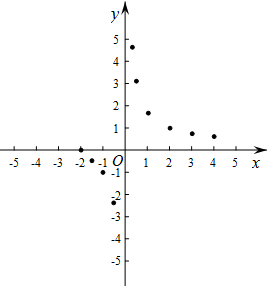18．有这样一个问题：探究函数y=$\frac{{\sqrt{x+2}}}{x}$的图象与性质．小美根据学习函数的经验，对函数y=$\frac{{\sqrt{x+2}}}{x}$的图象与性质进行了探究．下面是小美的探究过程，请补充完整：
（1）函数y=$\frac{{\sqrt{x+2}}}{x}$的自变量x的取值范围是x≥-2且x≠0；
（2）下表是y与x的几组对应值．

x	-2	-$\frac{3}{2}$	-1	-$\frac{1}{2}$	$\frac{1}{3}$	$\frac{1}{2}$	1	2	3	4	…
y	0	-$\frac{{\sqrt{2}}}{3}$	-1	-$\sqrt{6}$	$\sqrt{21}$	$\sqrt{10}$	$\sqrt{3}$	m	$\frac{{\sqrt{5}}}{3}$	$\frac{{\sqrt{6}}}{4}$	…

求m的值；
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的一条性质：当-2≤x＜0或x＞0时，y随x增大而减小．

科目： 来源： 题型：选择题

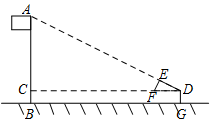17．如图，某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度，他们通过调整测量位置，使斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上，已知DE=0.5米，EF=0.25米，目测点D到地面的距离DG=1.5米，到旗杆的水平距离DC=20米，则旗杆的高度为（　　）

A．

10$\sqrt{5}$米

B．

（10$\sqrt{5}$+1.5）米

C．

11.5米

D．

10米

科目： 来源： 题型：选择题

科目： 来源： 题型：选择题

科目： 来源： 题型：选择题

科目： 来源： 题型：选择题

13．如图，点D，E分别在△ABC 的AB，AC边上，且DE∥BC，如果AD：AB=2：3，那么DE：BC等于（　　）

A．

3：2

B．

2：5

C．

2：3

D．

3：5

科目： 来源： 题型：解答题

12．“昊天塔”又称多宝佛塔，是北京地区惟一的楼阁式空心砖塔，位于良乡东北1公里的燎石岗上．此塔始建于隋，唐朝曾重修，现存塔是辽代修建的，已历经一千多年．某校九年级数学兴趣小组的同学进行社会实践活动时，想利用所学的解直角三角形的知识测量它的高度．他们的测量工具有：高度为1.5m的测角仪（测量仰角、俯角的仪器）、皮尺．请你帮他们设计一种测量方案，求出昊天塔的塔顶到地面的高度AB，注意：因为有护栏，他们不能到达塔的底部．
要求：（1）画出测量方案的示意图，标出字母，写出图中需要并且能测量的角与线段（用图中的字母表示）；
（2）结合示意图，简要说明你测量与计算的思路（不必写出结果）．

科目： 来源： 题型：解答题

11．我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段AB的最小覆盖圆就是以线段AB为直径的圆（图1）．
（1）在图2中作出锐角△ABC的最小覆盖圆（要求用尺规作图，保留作图痕迹，不写作法）；
（2）图3中，△ABC是直角三角形，且∠C=90°，请说明△ABC的最小覆盖圆圆心所在位置；
（3）请在图4中对钝角△ABC的最小覆盖圆进行探究，并结合（1）、（2）的结论，写出关于任意△ABC的最小覆盖圆的规律．

科目： 来源： 题型：解答题

10．已知：△ABC中，∠BAC=30°，AB=AC=4．将△ABC沿AC翻折，点B落在B′点，连接并延长A B′与线段BC的延长线相交于点D，求AD的长．