14．八年级（3）班开展了手工制作竞赛，每个同学都在规定时间内完成一件手工作品．陈莉同学在制作手工作品的第一、二个步骤是：①先裁下了一张长BC=20cm，宽AB=16cm的矩形纸片ABCD，②将纸片沿着直线AE折叠，点D恰好落在BC边上的F处，则EC的长为6 cm．

13．已知：如图，AB=CD，AE⊥BC，DF⊥BC，CE=BF．
求证：AB∥CD．

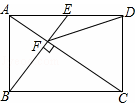12．如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF，分析下列五个结论：①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠CAD=$\sqrt{2}$；⑤S_{四边形CDEF}=$\frac{5}{2}$S_△ABF，其中正确的结论有①②③⑤．

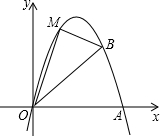11．如图，在平面直角坐标系中，己知点A（5，0），B（4，4）
（1）求过O、B、A三点的抛物线的解析式；
（2）在抛物线上求一点P（不同于点B），使S_△PAO=S_△ABO，请直接写出点P的坐标；
（3）在位于线段OB上方的抛物线上有一动点M，其横坐标为t，求△OBM的面积S和t的函数关系式；
（4）t为何值时，S_△OBM=$\frac{3}{5}$S_△ABO．

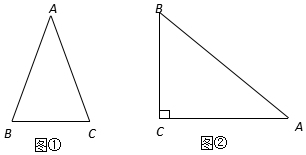10．通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图①在△ABC中，AB=AC，顶角A的正对记作sadA，这时sadA=$\frac{底边}{腰}=\frac{BC}{AB}$．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：
（1）sad60°=1．
（2）对于0°＜A＜180°，∠A的正对值sadA的取值范围是0＜sadA＜2．
（3）如图②，Rt△ABC中，已知sinA=$\frac{3}{5}$，其中∠A为锐角，试求sadA的值．

9．如图，已知∠COB=2∠AOC，OD平分∠AOB，∠AOC=20°，求∠COD的度数．

8．2014年宁波市举行“足球迷”杯足球比赛，共有奇数个足球队参加，每个队都同其他队比赛一场，记分办法为胜一场得1分、平一场得0.5分，负一场得0分．已知其中有两队共得10分，其他队的平均分为整数，求参加此次比赛的足球队共有几支？

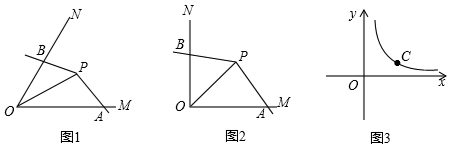7．如图1，点P为∠MON的平分线上一点，以P为顶点的角的两边分别与射线OM，ON交于A，B两点，如果∠APB绕点P旋转时始终满足OA•OB=OP²，我们就把∠APB叫做∠MON的智慧角．
（1）如图2，已知∠MON=90°，点P为∠MON的平分线上一点，以点P为顶点的角的两边分别与射线OM，ON交于A，B两点，且∠APB=135°．求证：∠APB是∠MON的智慧角；
（2）如图3，C是函数y=$\frac{3}{x}$（x＞0）图象上的一个动点，过点C的直线CD分别交x轴和y轴于点A，B两点，且满足BC=2CA，请求出∠AOB的智慧角∠APB的顶点P的坐标．

6．已知直线y=$\frac{4}{3}$x+8交x轴于A点，交y轴于B点，点C为OB的中点，点D在第二象限，且四边形AOCD为长方形．
（1）点D的坐标为（-6，4）；点E的坐标为（-3，4）．
（2）设直线AB与CD相交于点E，动点P从A点出发，以每秒2个单位长度的速度，沿AO、OC向点C作匀速运动，设点P的运动时间为t秒，
①△PAE的面积为S，请求出S关于t的函数关系式，并写出自变量t的取值范围；
②在动点P从A出发的同时，动点Q从C点出发，以每秒1个单位长度的速度，沿CE向点E作匀速运动，当P、Q中的一点到达终点后，该点停止运动，另一点继续运动，直至到达终点，整个运动停止．问：是否存在这样的t，使得直线PQ将四边形AOCE的面积分成1：3两部分？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．      

5．如图1，长方形ABCD中，∠A=∠B=∠C=∠D=90°，AB=CD，AD=BC，且$\sqrt{AB-4}$+|BC-6|=0，点P、Q分别是边AD、AB上的动点．
（1）求BD的长；
（2）如图2，在P、Q运动中是否能使△CPQ成为等腰直角三角形？若能，请求出PA的长；若不能，请说明理由；
（3）如图3，在BC上取一点E，使EC=5，那么当△EPC为等腰三角形时，请直接写出PA的长．