
科目: 来源: 题型:解答题
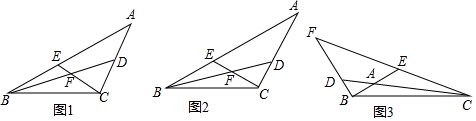
查看答案和解析>>
科目: 来源: 题型:选择题
 如图,⊙O的直径CD=12cm,AB是⊙O的弦,AB⊥CD,垂足为E,OE:OC=1:3,则AB的长为( )
如图,⊙O的直径CD=12cm,AB是⊙O的弦,AB⊥CD,垂足为E,OE:OC=1:3,则AB的长为( )| A. | 2$\sqrt{2}$cm | B. | 4$\sqrt{2}$cm | C. | 6$\sqrt{2}$cm | D. | 8$\sqrt{2}$cm |
查看答案和解析>>
科目: 来源: 题型:选择题
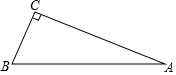 如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠A的正弦值为( )
如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠A的正弦值为( )| A. | $\frac{5}{12}$ | B. | $\frac{12}{13}$ | C. | $\frac{12}{5}$ | D. | $\frac{5}{13}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
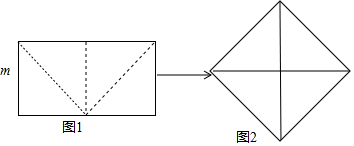
查看答案和解析>>
科目: 来源: 题型:解答题
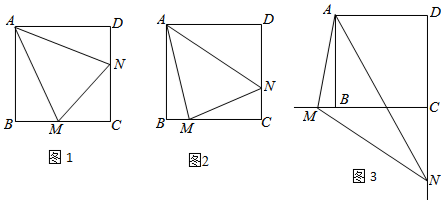
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的凸四边形叫做筝形.AC,BD叫作筝形的对角线.请你通过观察、测量、折纸等方法进行探究,并回答以下问题:
如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的凸四边形叫做筝形.AC,BD叫作筝形的对角线.请你通过观察、测量、折纸等方法进行探究,并回答以下问题:查看答案和解析>>
科目: 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8,半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3,将Rt△ABC绕点A顺时针旋转,设旋转角为α(0°≤α≤180°)
如图,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8,半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3,将Rt△ABC绕点A顺时针旋转,设旋转角为α(0°≤α≤180°)查看答案和解析>>
科目: 来源: 题型:解答题
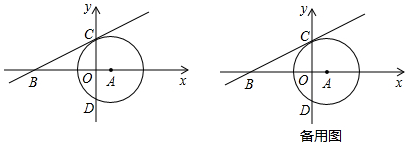
查看答案和解析>>
科目: 来源: 题型:解答题
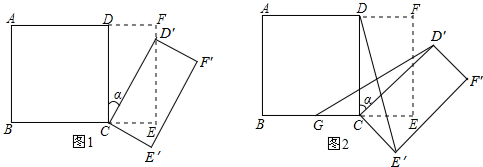
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com