4．将一副等腰直角三角板拼成如图（1）所示的图形（说明：三角板有一锐角为45°），连结AD、BE．
（1）BE与AD的数量关系是AD=BE（B、C、D在一条直线上）；
（2）图（2）是三角板绕C点旋转了个角度，此时BE与AD的数量关系是否有所改变？请说明理由．

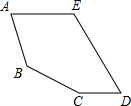3．聪聪用五根宽度相同的木条拼成了一个五边形，如图所示，已知AE∥CD，∠A=$\frac{1}{2}$∠C，∠B=120°，∠D=50°．
（1）求这个五边形的内角和；
（2）求∠A的度数；
（3）要使这个五边形始终保持这个状态，聪聪至少还需几根同宽度的木条？

2．有10个城市进行篮球比赛，每个城市均派3个代表队参加比赛，规定同一城市间代表队不进行比赛，其他代表队都要比赛一场，问按此规定，所有代表队要打多少场比赛？

1．如图，BD和EC相交于点A，ED∥BC，BD=12，AD=4，EC=9，则AC=？

20．如图，点D、E分别是△ABC的边AB，AC的中点，点F在DE的延长线上，且EF=DE．求证：
（1）BD=FC；
（2）AB∥CF．

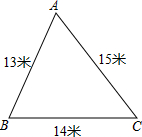19．学校校内有一块如图所示的三角形空地ABC，计划将这块空地建成一个花园，以美化校园环境，预计花园每平方米造价为30元，学校修建这个花园需要投资多少元？

18．如图，在△ABC中，∠A=50°，∠B=70°，点D在BC的延长线上，那么∠ACD=120°．

17．“吸烟有害健康！”国家为了加强对香烟产销的宏观管理，对销售香烟实行征收附加税政策，现在知道某品牌的香烟每条的市场价格为70元，不加收附加税时，每年销售110万条．若国家征收附加税，税率为x%（即每销售100元，征附加税x元），则每年的销售量将减少10x万条．要使每年对此项经营所收取附加税为168万元，问税率应确定为多少？

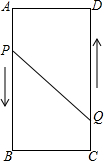16．A、B、C、D为矩形的四个顶点，AB=16cm，AD=6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，一直到达B为止，点Q以2cm/s的速度向D移动．
（1）P、Q两点从出发开始到几秒时四边形PBCQ是矩形？
（2）P、Q两点从出发开始到几秒时，点P和点Q的距离是10cm？

15．【阅读理解】当a＞0，b＞0时，a=（$\sqrt{a}$）²，b=（$\sqrt{b}$）²则（$\sqrt{a}$-$\sqrt{b}$）²=（$\sqrt{a}$）²-2$\sqrt{ab}$+（$\sqrt{b}$）²=a+b-2$\sqrt{ab}$≥0，那么$\frac{a+b}{2}$≥$\sqrt{ab}$，因此对任意两个正数a，b，即a＞0，b＞0，则有下面的不等式；$\frac{a+b}{2}$$≥\sqrt{ab}$，当且仅当a=b时取等号，我们把$\frac{a+b}{2}$叫做正数a，b的算术平均数，把$\sqrt{ab}$叫做正数a，b的几何平均数，于是上述的不等式可以表述为：两个正数的算术平均数不小于（即大于或等于）他们的几何平均数，它在数学中有广泛的应用，是解决最大（小）值问题的有力工具．
【实例剖析】已知x＞0，求式子y=x+$\frac{4}{x}$的最小值．
解：令a=x，b=$\frac{4}{x}$，则由$\frac{a+b}{2}$≥$\sqrt{ab}$，得y=x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$=2×$\sqrt{4}$=4，当且仅当x=$\frac{4}{x}$时，即x=2时，式子的最小值，最小值为4．
【学以致用】根据上面的阅读材料回答下列问题：
（1）已知x＞0，则当x为$\frac{\sqrt{6}}{2}$时，式子y=2x+$\frac{3}{x}$取到最小值，最小值是2$\sqrt{6}$．
（2）用篱笆围一个面积为64m²的矩形花园，问这个矩形的长、宽各为多少时，所用的篱笆最短，最短是多少米？
（3）已知x＞0，则当x取何值时，式子y=$\frac{x}{{x}^{2}-2x+9}$取到最大值，最大值是多少？