16．某镇正在建造的文化广场工地上，有两种铺设广场地面的材料：一种是长为a cm，宽为b cm的长方形板材（如图1），另一种是边长为C cm的正方形地砖（图2）．

（1）用多少块如图2所示的正方形地砖能拼出一个新的正方形？（只要写出一个符合条件的答案即可），并写出新正方形的面积；
（2）用如图1所示的四块长方形板材铺成如图3的大长方形或如图4的大正方形，中间分别空出一个小长方形和小正方形（即图中阴影部分）；
①试比较中间的小长方形和中间的小正方形的面积哪个大？大多少？
②如图4，已知大正方形的边长比中间的小正方形的边长多20cm，面积大3200cm²．如果选用如图2所示的正方形地砖（边长为20cm）铺设图4中间的小正方形部分，那么能否做到不用切割地砖就可直接密铺（缝隙忽略不计）呢？若能，请求出密铺所需地砖的块数；若不能，至少要切割几块如图2的地砖？

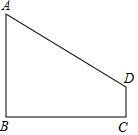15．如图，AB⊥BC，DC⊥BC，垂足分别为B、C，设AB=4，DC=1，BC=4．
（1）求线段AD的长．
（2）在线段BC上是否存在点P，使△APD是等腰三角形？若存在，求出线段BP的长；若不存在，请说明理由．

14．如图，AB和CD交于点O，AO=2，OD=3，OC=4，OB=6，求证：∠A=∠D．

13．下列函数关系不是一次函数的是（　　）

	A．	汽车以120Km/h的速度匀速行驶，行驶路程y（Km）与时间t（h）之间的关系
	B．	等腰三角形顶角y与底角x间的关系
	C．	高为4cm的圆锥体积y （cm3）与底面半径x （cm）的关系
	D．	一棵树现在高50cm，每月长高3cm，x个月后这棵树的高度y （cm）与生长月数x（月）之间的关系

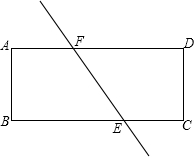12．如图，直线EF将矩形纸片ABCD分成面积相等的两部分，E、F分别与BC交于点E，与AD交于点F（E，F不与顶点重合）．设AB=a，AD=b，BE=x．用剪刀将纸片沿直线EF剪开后，将纸片ABEF沿AB翻折，再平移拼接在梯形ECDF的下方，那么能否做到纸片ABEF的一边与EC重合，另一边落在DC的延长线上，能（用“能”或“不能”填空）．若填“能”，我们把拼接后在下方的四边形记作ECB′E′，当$\frac{x}{b}$的值为$\frac{2}{3}$或$\frac{1}{3}$时，直线E′E经过原矩形的一个顶点，若填“不能”，请说明理由：不能．

11．如图，AB为⊙O的弦，AB=6，点C是⊙O上的一个动点，且△ACB=45°，若点M、N分别是AB、BC的中点，求MN长的最大值．

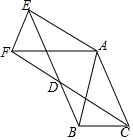10．△ABC中，AB=AC=1，∠BAC=45°，将△ABC绕点A按顺时针旋转α得到△AEF，连接BE，CF，它们交于D点，
①求证：BE=CF．
②当α=120°，求∠FCB的度数．
③当四边形ACDE是菱形时，求BD的长．

9．长为1，宽为a的矩形纸片（0＜a＜$\frac{1}{2}$），如图那样折一下，剪下一个边长等于矩形宽度的正方形（称为第一次操作）；再把剩下的矩形如图那样折一下，剪下一个边长等于此时矩形宽度的正方形（称为第二次操作）；如此反复操作下去．若在第n次操作后，剩下的矩形为正方形，则操作终止．当n=3时，a的值为$\frac{3}{5}$或$\frac{3}{4}$．

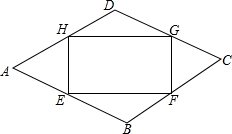8．如图，点E、F、G、H分别在菱形ABCD的四条边上，且BE=BF=DG=DH，连接EF，FG，GH，HE得到四边形EFGH，∠A=60°．设AE=x，四边形EFGH的面积为s与边AE的关系为s=-$\sqrt{3}{x}^{2}$+4$\sqrt{3}$x，则菱形边长为4．

7．设等腰三角形的三条边长分别为a、b、c，已知a=2，b、c是关于x的方程x²-10x+m=0的两个根，求m的值．