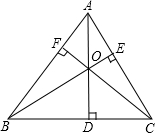6．如图，△ABC的三条高AD、BE、CF相交于点O．
（1）在△BOC中，OB边上的高是CE，OC边上的高是BF，BC边上的高是OD．
（2）在△AOC中，OA边上的高是CD，OC边上的高是AF，AC边上的高是OE．
（3）在△AOB中，OA边上的高是BD，OB边上的高是AE，AB边上的高是OF．

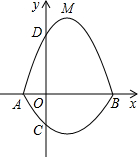5．如图所示，在平面直角坐标系中，A、B为x轴上两点，C、D为y轴上两点，经过点A，C，B的抛物线的一部分C₁与经过点A，D，B的抛物线的一部分C₂组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．
已知点C的坐标为（0，-$\frac{3}{2}$），点M是抛物线C₂：y=mx²-2mx-3m（m＜0）的顶点
（1）求A、B两点的坐标；
（2）求经过点A，C，B的抛物线C₁的函数表达式．
（3）探究“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出点P的坐标及△PBC面积的最大值；若不存在，请说明理由．

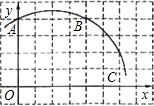4．如图，已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C．
（1）用直尺画出该圆弧所在圆的圆心M的位置并写出点M的坐标；
（2）若A点的坐标为（0，4），D点的坐标为（7，0），求证直线CD是⊙M的切线．

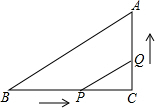3．如图所示，∠C=90°，BC=8cm，AC=6cm，点P从点B出发，沿BC向点C以2cm/s的速度移动，点Q从点C出发沿CA向点A以1cm/s的速度移动，如果P、Q分别从B、C同时出发，过多少时，以C、P、Q为顶点的三角形恰与△ABC相似？

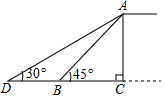2．某市为缓解城市交通压力，决定修建人行天桥．原设计天桥的楼梯长AB=6m，∠ABC=45°，后考虑到安全因素，将楼梯脚B移到CB延长线上点D处，使∠ADC=30°．求BD的长．（结果保留根号）．

1．已知关于x的方程（1-m）x²+4x+1=0有两个不相等的实数根，则m的取值范围是m＞-3且m≠1．

20．阅读理解．
若方程x²+px+q=0的根为x₁=a、x₂=b，则a+b=-p、ab=q，所以x²+px+q=x²-（a+b）x+ab=（x-a）（x-b），也就是说如果知道x²+px+q=0的两根就可以对x²+px+q分解因式了．例如在实数范围内分解x²-x-1
解：设x²-x-1=0解得x=$\frac{1±\sqrt{5}}{2}$则x²-x-1=（x-$\frac{1+\sqrt{5}}{2}$）（x-$\frac{1-\sqrt{5}}{2}$）
（1）在实数范围内分解二次三项式：y²-3y-2
（2）试分解2x²+x-4
（3）探索：二次三项式ax²+bx+c（a≠0、a、b、c是常数）满足什么条件时，在实数范围内可分解因式，满足什么条件时，不能在实数范围内分解因式．

19．x、y均为实数y＜$\sqrt{x-1}$+$\sqrt{1-x}$+$\frac{1}{2}$，化简：$\frac{\sqrt{（1-y）^{2}}}{y-1}$．

18．（1）-1⁴+$\frac{1}{\sqrt{2}-1}$+$\sqrt{3}$（$\sqrt{3}$-$\sqrt{6}$）+$\sqrt{8}$
（2）（x-1）（x+2）=1
（3）（2$\sqrt{3}$+3$\sqrt{2}$-$\sqrt{6}$）（2$\sqrt{3}$-3$\sqrt{2}$+$\sqrt{6}$）        
（4）3（x-3）²-27=0．

17．在函数y=$\frac{\sqrt{4x-3}}{x-2}$中，自变量x的取值范围是x≥$\frac{3}{4}$且x≠2．