9.(1)观察发现:
材料:解方程组$\left\{\begin{array}{l}{x+y=4①}\\{3(x+y)+y=14②}\end{array}\right.$
将①整体代入②,得3×4+y=14,
解得y=2,
把y=2代入①,得x=2,
所以$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$
这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此方法解答,
请直接写出方程组$\left\{\begin{array}{l}{x-y-1=0,①}\\{4(x-y)-y=5,②}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$
(2)实践运用:请用“整体代入法”解方程组
$\left\{\begin{array}{l}{2x-3y-2=0,①}\\{\frac{2x-3y+5}{7}+2y=9,②}\end{array}\right.$
(3)拓展运用:若关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x+y=-3m+2}\\{x+2y=4}\end{array}\right.$的解满足x+y>$-\frac{2}{3}$,请直接写出满足条件的m的所有正整数值1,2.

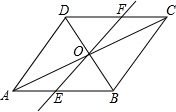 如图,在平行四边形ABCD中,对角线AC与BD交于点O,经过点O的直线交AB于E,交CD于F,连接DE、BF
如图,在平行四边形ABCD中,对角线AC与BD交于点O,经过点O的直线交AB于E,交CD于F,连接DE、BF