
科目: 来源: 题型:解答题
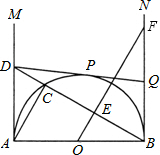 如图,AB是半圆O的直径,AB=2,射线AM、BN为半圆的切线,在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点作半圆的切线DP,切点为P,与BN相交于点Q.
如图,AB是半圆O的直径,AB=2,射线AM、BN为半圆的切线,在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点作半圆的切线DP,切点为P,与BN相交于点Q.查看答案和解析>>
科目: 来源: 题型:选择题
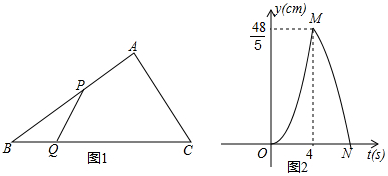
| A. | ①②④ | B. | ②③④ | C. | ①③④ | D. | ①②③ |
查看答案和解析>>
科目: 来源: 题型:解答题
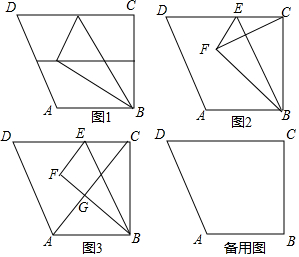
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,$\sqrt{3}$≈1.7).
如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,$\sqrt{3}$≈1.7).查看答案和解析>>
科目: 来源: 题型:选择题
| A. | -m8n4 | B. | mn4 | C. | -m9n | D. | 5m3n2 |
查看答案和解析>>
科目: 来源: 题型:填空题
 抛物线y=x2+2mx+$\frac{{m}^{2}}{4}$(m<0)的顶点为P,抛物线与x轴的交点为A、B,当△PAB是等边三角形时,m的值为-2.
抛物线y=x2+2mx+$\frac{{m}^{2}}{4}$(m<0)的顶点为P,抛物线与x轴的交点为A、B,当△PAB是等边三角形时,m的值为-2.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com