科目： 来源： 题型：解答题

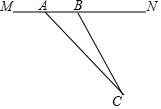18．目前，我市正在积极创建文明城市，交通部门一再提醒司机：为了安全，请勿超速，并再进一步完善各类监测系统，如图，在某公路直线路段MN内限速60千米/小时，为了检测车辆是否超速，在公路MN旁设立了观测点C，从观测点C测得一小车从点A到达点B行驶了5秒钟，已知∠CAN=45°，∠CBN=60°，BC=200米，此车超速了吗？请说明理由．（参考数据：$\sqrt{2}$=1.41，$\sqrt{3}$=1.73）

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

16．如图1，在△ABC中，CA=CB，∠ACB=90°，D是△ABC内部一点，∠ADC=135°，将线段CD绕点C逆时针旋转90°，得到线段CE，连接DE；
（1）①依据题意补全图形；②请判断∠ADC和∠CDE之间的数量关系为∠ADC+∠CDE=180°；
（2）在（1）的条件下，连接BE，过点C作CM⊥DE，请判断线段CM、AE和BE之间的敦量关系，并说明理由；
（3）在（1）的条件下，若AD=1，CD=$\sqrt{2}$，BC边的中点为P，点G是线段DE上一个动点，当△CDE绕点C旋转的过程中，则PG的最小值为0；PG的最大值为$\sqrt{2}$+$\frac{\sqrt{5}}{2}$．

科目： 来源： 题型：解答题

15．【问题提出】如图1．△ABC是等边三角形，点D在线段AB上．点E在直线BC上．且∠DEC=∠DCE．求证：BE=AD；
【类比学习】如图2．将条件“点D在线段AB上”改为“点D在线段AB的延长线上”，其他条件不变．判断线段AB、BE、BD之间的数量关系，并说明理由．
【扩展探究】如图3．△ABC是等腰三角形，AB=AC，∠BAC=120°，点D在线段AB的反向延长线上，点E在直线BC上，且∠DEC=∠DCE，【类比学习】中的线段AB、BE、BD之间的数量关系是否还成立？若成立，请说明理由；若不成立，请直接写出线段AB，BE，BD之间的数量．

科目： 来源： 题型：解答题

14．如图1，已知线段AB的两个端点坐标分别为A（a，1），B（-2，b），且满足$\sqrt{a+5}$+$\sqrt{b-3}$=0．
（1）则a=-5，b=3；
（2）在y轴上是否存在点C，使三角形ABC的面积等于8？若存在，请求出点C的坐标；若不存在，请说明理由；
（3）如图2，将线段BA平移得到线段OD，其中B点对应O点，A点对应D点，点P（m，n）是线段OD上任意一点，求证：3n-2m=0．

科目： 来源： 题型：解答题

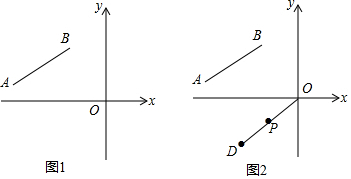
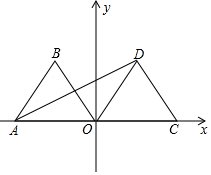13．如图，在平面直角坐标系中，点A（-2，0），等边△AOB经过平移或轴对称或旋转都可以得到△OCD．
（1）填空：
①△AOB沿x轴向右平移得到△OCD，则平移的距离是2个单位长度；
②△AOB与△OCD关于某直线对称，则对称轴是y轴；
③△AOB绕原点O顺时针旋转得到△OCD，则旋转角度可以是120度；
（2）连接AD，请探索AD与CD的位置关系．

科目： 来源： 题型：填空题

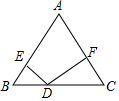12．如图，在等腰三角形△ABC中，AB=AC=5，BC=6，D为底边BC上一动点（不与B、C重合）DE⊥AB，DF⊥AC，垂足分别为E、F，则DE+DF=$\frac{24}{5}$．

科目： 来源： 题型：选择题

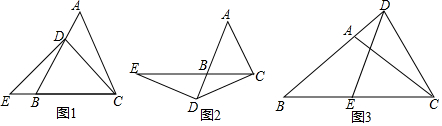
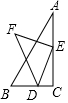11．一副三角形板按如图摆放在桌面上，已知∠ACB=∠DEF=90°，点D在BC边上，点E在AC边上，当点D从点B向点C运动过程中，则F，C两点之间的距离变化情况是（　　）

A．

一直增大

B．

一直减小

C．

先减小后增大

D．

先增大后减小

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

9．如图（1），在平面直角坐标系中，点A，B的坐标分别为（-1，0），（3，0），将线段AB先向上平移2个单位长度，再向右平移1个单位长度，得到线段CD，连接AC，BD，构成平行四边形ABDC．
（1）请写出点C的坐标为（0，2），点D的坐标为（4，2），S_{四边形ABDC}8；
（2）点Q在y轴上，且S_△QAB=S_{四边形ABDC}，求出点Q的坐标；
（3）如图（2），点P是线段BD上任意一个点（不与B、D重合），连接PC、PO，试探索∠DCP、∠CPO、∠BOP之间的关系，并证明你的结论．