科目： 来源： 题型：填空题

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

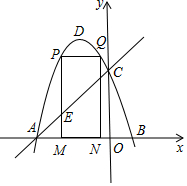2．如图，抛物线y=-x²-2x+3的图象与x轴交A、B两点，与y轴交于点C，点D为抛物线的顶点．
（1）求点A、B、C的坐标；
（2）点M为线段AB上一点（点M不与点A、B重合），过M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过P作PQ∥AB交抛物线于点Q，过Q作QN⊥x轴于N，当矩形PMNQ的周长最大时，求△AEM的面积；
（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ，过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方），若FG=2$\sqrt{2}$DQ，求点F的坐标．

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

20．如图，已知AB是⊙O的直径，C是⊙O上的点，且OE⊥AC于点E，过点C作⊙O的切线，交OE的延长线于点D，交AB的延长线于点F，连接AD
（1）求证：AD是⊙O的切线；
（2）若tan∠F=$\frac{1}{2}$，⊙O半径为1，求线段AD的长．

科目： 来源： 题型：解答题

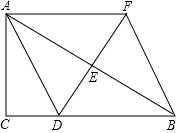19．如图，在△ABC中，∠C=90°，点D为边BC上一点，点E为边AB的中点，过点A作AF∥BC，交DE的延长线与点F，连接BF．
（1）求证：四边形ADBF是平行四边形；
（2）若∠ADF=∠BDF，DF=2CD，求∠ABC的度数．

科目： 来源： 题型：解答题

18．某学校准备开展“阳光体育活动”，决定开设以下体育活动项目：足球、乒乓球、篮球和羽毛球，要求每位学生必须且只能选择一项，为了解选择各种体育活动项目的学生人数，随机抽取了部分学生进行调查，并将通过调查获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据统计图回答问题：
（1）这次活动一共调查了250名学生；
（2）补全条形统计图，并求出扇形统计图中选择篮球项目的人数所在扇形的圆心角的度数；
（4）若该学校有1200人，则该学校选择足球项目的学生人数约是多少？

科目： 来源： 题型：解答题

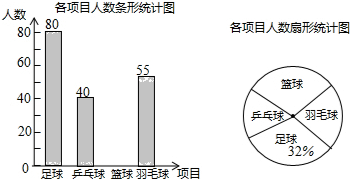
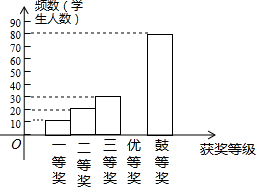17．为了进一步普及足球知识，传播足球文化，我市举行了“足球进校园”知识竞赛活动，为了解足球知识的普及情况，随机抽取了部分获奖情况进行整理，得到下列不完整的统计图表：

获奖等次	频数	频率
一等奖	10	0.05
二等奖	20	0.10
三等奖	30	b
优胜奖	a	0.30
鼓励奖	80	0.40

请根据所给信息，解答下列问题：
（1）a=60，b=0.15，且补全频数分布直方图；
（2）若用扇形统计图来描述获奖分布情况，问获得优胜奖对应的扇形圆心角的度数是多少？
（3）若我市初中生共有16000人，竞赛活动获奖率为40%，获三等奖以上的学生表示对“足球比较喜欢”，请你估计我市初中生对“足球比较喜欢”的有多少人？

科目： 来源： 题型：解答题

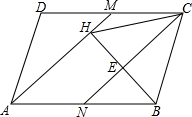16．如图，已知点M、N分别为?ABCD的边CD、AB的中点，连接AM、CN．
（1）证明：AM=CN；
（2）过点B作BH⊥AM于点H，交CN于点E，连接CH，判断线段CB、CH的数量关系，并说明理由．

科目： 来源： 题型：解答题