20．若二次函数y=ax²-2ax+c的图象经过点（-1，0），则方程ax²-2ax+c=0的解为x=-1．

19．如果函数y=2x²-3ax+1，在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为-23，则a的值为（　　）

A．

$\frac{26}{3}$

B．

$3\sqrt{2}$

C．

$\frac{8\sqrt{3}}{3}$或$\frac{14}{3}$

D．

$\frac{14}{3}$

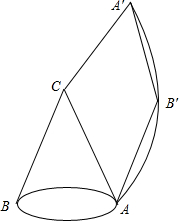18．如图，沿纸筒圆锥的母线CA剪开展开，点A对应点为A′，点B对应点为B′，连接A′B′，B′A，四边形CA′B′A恰好是个菱形，若CA=6cm，则圆锥的底面积为4π（结果保留π）．

17．如图，有足够多的边长为a的小正方形（A类）、长为a宽为b的长方形（B类）以及边长为b的大正方形（C类），发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式． 比如图②可以解释为：（a+2b）（a+b）=a²+3ab+2b² ．

（1）取图①中的若干个（三种图形都要取到）拼成一个长方形，使它的边长分别为（2a+b）、（a+2b），不画图形，试通过计算说明需要C类卡片多少张；
（2）若取其中的若干个（三种图形都要取到）拼成一个长方形，使它的面积等于a²+5ab+4b²，画出这个长方形，并根据图形对多项式a²+5ab+4b²进行因式分解；
（3）如图③，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个矩形的两边长（x＞y），观察图案并判断，将正确关系式的序号填写在横线上①②③④（填写序号）．
①xy=$\frac{{m}^{2}-{n}^{2}}{4}$      ②x+y=m   ③x²-y²=m•n     ④x²+y²=$\frac{{m}^{2}+{n}^{2}}{2}$．

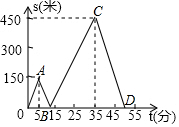16．甲、乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走，设甲、乙两人相距s（米），甲行走的时间为t（分），s关于t的函数图象如图所示．
（1）求乙出发多长时间后能追上甲？
（2）求直线BC的函数表达式；
（3）当甲、乙两人相距330米时，求t的值．

15．如图1，在△ABC中，∠ABC与∠ACB的角平分线交于O点．
（1）若∠A=40°，则∠BOC=110°；
（2）若∠A=n°，则∠BOC=90+$\frac{n}{2}$°；
（3）若∠A=n°，∠ABC与∠ACB的角平分线交于O点，∠ABO的平分线与∠ACO的平分线交于点O₁，…，∠ABO₂₀₁₆的平分线与∠ACO₂₀₁₆的平分线交于点O₂₀₁₇，则∠O₂₀₁₇=$\frac{1}{{2}^{2018}}$×180°+$\frac{{2}^{2018}-1}{{2}^{2018}}$n°．

14．已知x的立方根是3，求2x+10的算术平方根．

13．解方程组：
（1）$\left\{\begin{array}{l}{x+2y=1，①}\\{3x-2y=11②}\end{array}\right.$
（2）$\left\{\begin{array}{l}{\frac{m}{2}+\frac{n}{3}=13}\\{\frac{m}{3}-\frac{n}{4}=3}\end{array}\right.$．

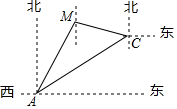12．一渔船在海岛A北偏东30°方向的M处遇险，渔船将险情报告给位于A处的救援船后，沿南偏东75°方向向海岛C靠近，同时，从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行，30分钟后，救援船在海岛C处恰好追上渔船，那么渔船遇险M处与海岛C的距离是多少海里？（$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7，$\sqrt{6}$≈2.4）

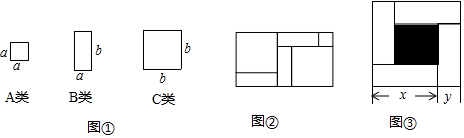
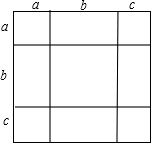11．把几个图形拼成一个新的图形，再通过图形面积的计算，常常可以得到一些有用的式子，如图，是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形．
①若用不同的方法计算这个边长为a+b+c的正方形面积，
就可以得到一个等式，①这个等式可以为（a+b+c）²=a²+b²+c²+2ab+2bc+2ac．（只要写出一个即可）
请利用①中的等式解答下列问题：
②若a，b，c三个数满足a²+b²+c²=29，ab+bc+ac=26，
则（a+b+c）²=81．
③因式分解：a²+4b²+9c²+4ab-12bc-6ac=（a+2b+3c）²．