10．一个不透明的口袋里装有红、黄、绿三种颜色的小球（除颜色不同外其余都相同），其中红球2个（分别标有1号、2号），黄球1个，从中任意摸出1球是绿球的概率是$\frac{1}{4}$．
（1）试求口袋中绿球的个数；
（2）小明和小刚玩摸球游戏：第一次从口袋中任意摸出1球（不放回），第二次再摸出1球．两人约定游戏胜负规则如下：摸出“一绿一黄”，则小明赢；摸出“一红一黄”，则小刚赢．你认为这种游戏胜负规则公平吗？请用列表或画树状图的方法说明理由；若你认为不公平，请修改游戏胜负规则，使游戏变得公平．

9．有这样一个问题：探究同一平面直角坐标系中系数互为倒数的正、反比例函数y=$\frac{1}{k}$x与y=$\frac{k}{x}$（k≠0）的图象性质．
小明根据学习函数的经验，对函数y=$\frac{1}{k}$x与y=$\frac{k}{x}$，当k＞0时的图象性质进行了探究．
下面是小明的探究过程：
（1）如图所示，设函数y=$\frac{1}{k}$x与y=$\frac{k}{x}$图象的交点为A，B，已知A点的坐标为（-k，-1），则B点的坐标为（k，1）；
（2）若点P为第一象限内双曲线上不同于点B的任意一点．
①设直线PA交x轴于点M，直线PB交x轴于点N．求证：PM=PN．
证明过程如下：设P（m，$\frac{k}{m}$），直线PA的解析式为y=ax+b（a≠0）．
则$\left\{\begin{array}{l}{-ka+b=-1}\\{ma+b=\frac{k}{m}}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=}\\{b=}\end{array}\right.$$\frac{1}{m}$
$\frac{k}{m}$-1
∴直线PA的解析式为y=$\frac{1}{m}$x+$\frac{k}{m}$-1
请你把上面的解答过程补充完整，并完成剩余的证明．
②当P点坐标为（1，k）（k≠1）时，判断△PAB的形状，并用k表示出△PAB的面积．

8．如图，已知Rt△ABC，∠C=90°，D为BC的中点，以AC为直径的⊙O交AB于点E．
（1）求证：DE是⊙O的切线；
（2）若AE：EB=1：2，BC=6，求AE的长．

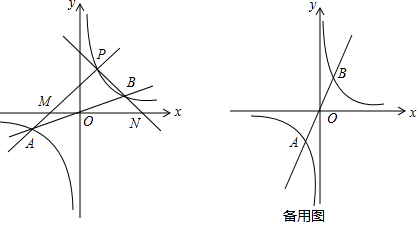
7．如图放置的两个正方形，大正方形ABCD边长为a，小正方形CEFG边长为b（a＞b），M在BC边上，且BM=b，连接AM，MF，MF交CG于点P，将△ABM绕点A旋转至△ADN，将△MEF绕点F旋转至△NGF，给出以下五个结论：①∠MAD=∠AND；②CP=b-$\frac{{b}^{2}}{a}$；③△ABM≌△NGF；④S_{四边形AMFN}=a²+b²；⑤A，M，P，D四点共圆，其中正确的个数是（　　）

A．

2

B．

3

C．

4

D．

5

6．下列函数中，对于任意实数x₁，x₂，当x₁＞x₂时，满足y₁＜y₂的是（　　）

A．

y=-3x+2

B．

y=2x+1

C．

y=2x2+1

D．

y=-$\frac{1}{x}$

5．一只不透明袋子中装有2个红球、1个黄球，这些球除颜色外都相同．小明搅匀后从中任意摸出一个球，记录颜色后放回、搅匀，再从中任意摸出1个球．则两次摸出的球都是黄球的概率是$\frac{1}{9}$．

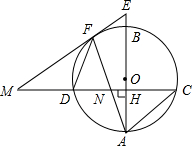4．如图，已知AB是圆O的直径，弦CD⊥AB，垂足为H，与AC平行的圆O的一条切线交CD的延长线于点M，交AB的延长线于点E，切点为F，连接AF交CD于点N．
（1）求证：CA=CN；
（2）连接DF，若cos∠DFA=$\frac{4}{5}$，AN=2$\sqrt{10}$，求圆O的直径的长度．

3．红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查，从试验田中随机抽取了30株，得到的数据如下（单位：颗）：

182	195	201	179	208	204	186	192	210	204
175	193	200	203	188	197	212	207	185	206
188	186	198	202	221	199	219	208	187	224

（1）对抽取的30株水稻稻穗谷粒数进行统计分析，请补全下表中空格，并完善直方图：

谷粒颗数	175≤x＜185	185≤x＜195	195≤x＜205	205≤x＜215	215≤x＜225
频数	3	8	10	6	3
对应扇形 图中区域	B	D	E	A	C

如图所示的扇形统计图中，扇形A对应的圆心角为72度，扇形B对应的圆心角为36度；
（2）该试验田中大约有3000株水稻，据此估计，其中稻穗谷粒数大于或等于205颗的水稻有多少株？

2．同时抛掷两枚质地均匀的骰子，则事件“两枚骰子的点数和小于8且为偶数”的概率是$\frac{1}{4}$．

1．问题背景
如图1，在正方形ABCD的内部，作∠DAE=∠ABF=∠BCG=∠CDH，根据三角形全等的条件，易得△DAE≌△ABF≌△BCG≌△CDH，从而得到四边形EFGH是正方形．
类比探究
如图2，在正△ABC的内部，作∠BAD=∠CBE=∠ACF，AD，BE，CF两两相交于D，E，F三点（D，E，F三点不重合）

（1）△ABD，△BCE，△CAF是否全等？如果是，请选择其中一对进行证明．
（2）△DEF是否为正三角形？请说明理由．
（3）进一步探究发现，△ABD的三边存在一定的等量关系，设BD=a，AD=b，AB=c，请探索a，b，c满足的等量关系．