
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
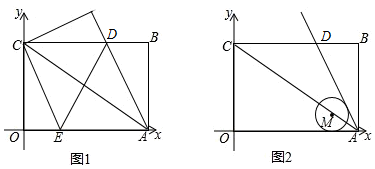
 如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,-1).
如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,-1).查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
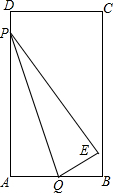 如图,矩形纸ABCD,AB=3,AD=6,动点Q从点A出发以每秒1个单位长的速度沿AB向终点B运动,运动$\frac{2}{3}$秒时,动点P从点D出发以相等的速度沿DA向终点A运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).将△APQ沿PQ翻折,得到△EPQ
如图,矩形纸ABCD,AB=3,AD=6,动点Q从点A出发以每秒1个单位长的速度沿AB向终点B运动,运动$\frac{2}{3}$秒时,动点P从点D出发以相等的速度沿DA向终点A运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).将△APQ沿PQ翻折,得到△EPQ查看答案和解析>>
科目: 来源: 题型:填空题
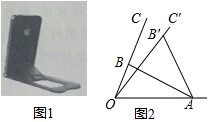 如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在OC上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达OC′的位置.已知OA=8cm,AB⊥OC,∠BOA=60°,sin∠B′AO=$\frac{9}{10}$,则点B′到OA的距离$\frac{18\sqrt{3}}{5}$cm.
如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在OC上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达OC′的位置.已知OA=8cm,AB⊥OC,∠BOA=60°,sin∠B′AO=$\frac{9}{10}$,则点B′到OA的距离$\frac{18\sqrt{3}}{5}$cm.查看答案和解析>>
科目: 来源: 题型:填空题
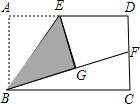 如图,在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,若DF=CF,则$\frac{AD}{AB}$的值$\sqrt{2}$.
如图,在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,若DF=CF,则$\frac{AD}{AB}$的值$\sqrt{2}$.查看答案和解析>>
科目: 来源: 题型:填空题
 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的纵坐标为1.
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的纵坐标为1.查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com