科目： 来源： 题型：填空题

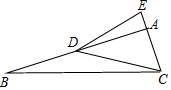20．已知：如图，在△ABC中，∠BAC=90°，点D在AB上，点E在CA的延长线上，连接DC、DE，∠EDC=45°，BD=EC，DE=5$\sqrt{2}$，tan∠DCE=$\frac{3}{13}$，则CE=$\frac{5\sqrt{18}}{3}$．

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

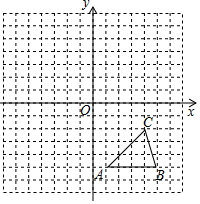18．如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，-2）．
（1）把△ABC向上平移5个单位后得到对应的△A₁B₁C₁，画出△A₁B₁C₁，并写出C₁的坐标；
（2）以原点O为对称中心，画出△ABC关于原点O对称的△A₂B₂C₂，并写出点C₂的坐标．

科目： 来源： 题型：解答题

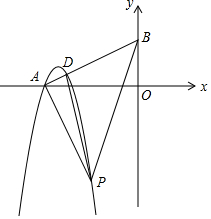17．已知抛物线C：y=（x+2）[t（x+1）-（x+3）]，其中-7≤t≤-2，且无论t取任何符合条件的实数，点A，P都在抛物线C 上．
（1）当t=-5 时，求抛物线C的对称轴；
（2）当-60≤n≤-30 时，判断点（1，n）是否在抛物线C上，并说明理由；
（3）如图，若点A在x轴上，过点A作线段AP的垂线交y轴于点B，交抛物线C于点D，当点D的纵坐标为m+$\frac{1}{2}$时，求S_△PAD的最小值．

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

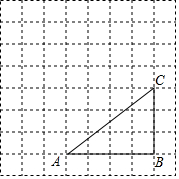15．如图，将△ABC放在由小正方形构成的网格图中，点A、B、C均落在格点上．
（1）请用无刻度的直尺画出∠ACB的平分线；
（2）以点C为旋转中心，把△ABC顺时针旋转，得到△A′B′C′，使点B的对应点B′恰好落在边AC上，请在如图所示的网格中，用无刻度的直尺，作出点B′．

科目： 来源： 题型：解答题

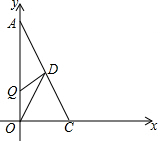14．如图，以直角三角形AOC的直角顶点O为原点，以OC、OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足$\sqrt{a-2b}$+|b-2|=0．
（1）则C点的坐标为（2，0）；A点的坐标为（0，4）．
（2）已知坐标轴上有两动点P、Q同时出发，P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动，Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动，点Q到达A点整个运动随之结束．AC的中点D的坐标是（1，2），设运动时间为t（t＞0）秒．问：是否存在这样的t，使S_△ODP=S_△ODQ？若存在，请求出t的值；若不存在，请说明理由．

科目： 来源： 题型：解答题

13．定义：对于平面直角坐标系中的任意直线MN及点P，取直线MN上一点Q，线段PQ与直线MN成30°角的长度称为点P到直线MN的30°角的距离，记作d（P→MN）．
已知O为坐标原点，A（4，0），B（3，3）是平面直角坐标系中两点．根据上述定义，解答下列问题：
（1）点A到直线OB的30°角的距离d（A→OB）=4$\sqrt{2}$；
（2）已知点G到线段OB的30°角的距离d（G→OB）=2，且点G的横坐标为1，则点G的纵坐标为1+$\sqrt{2}$或1-$\sqrt{2}$．．
（3）若点A到直线l：y=kx+1的30°角的距离d（A→l）=4，求k的值．

科目： 来源： 题型：选择题

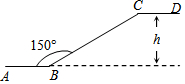12．某商场一楼与二楼之间的手扶电梯如图所示．其中AB、CD分别表示一楼、二楼地面的水平线，∠ABC=150°，BC的长是8m，则乘电梯从点B到点C上升的高度h是（　　）

A．

4$\sqrt{3}$m

B．

8m

C．

$\frac{8}{3}$$\sqrt{3}$m

D．

4m

科目： 来源： 题型：解答题

11．在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．
（1）当直线MN绕点C旋转到图1的位置时
①请说明△ADC≌△CEB的理由；
②请说明DE=AD+BE的理由；
（2）当直线MN绕点C旋转到图2的位置时，DE、AD、BE具有怎样的等量关系？请直接在横线上写出这个等量关系：DE=AD-BE
（3）当直线MN绕点C旋转到图3的位置时，DE、AD、BE具有怎样的等量关系？请直接在横线上写出这个等量关系：DE=BE-AD．