
科目: 来源: 题型:选择题
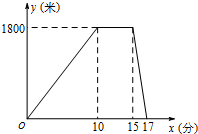 某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )
某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )| A. | 小明在公园休息了15分钟 | B. | 小明乘出租车用了17分 | ||
| C. | 小明跑步的速度为120米/分 | D. | 出租车的平均速度是900米/分 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
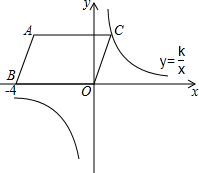 如图,在平面直角坐标系中,四边形ABOC为平行四边形,A、B的坐标分别为(-3,3),(-4,0).若有一双曲线y=$\frac{k}{x}$的图象经过点C,则这条双曲线的表达式为y=$\frac{3}{x}$.
如图,在平面直角坐标系中,四边形ABOC为平行四边形,A、B的坐标分别为(-3,3),(-4,0).若有一双曲线y=$\frac{k}{x}$的图象经过点C,则这条双曲线的表达式为y=$\frac{3}{x}$.查看答案和解析>>
科目: 来源: 题型:解答题
| 时间t(天) | 1 | 5 | 9 | 13 | 17 | 21 |
| 日销售量y(件) | 118 | 110 | 102 | 94 | 86 | 78 |
查看答案和解析>>
科目: 来源: 题型:解答题
| 车型 | 载货能力(箱/辆) | 运费 | |
| 甲村(元/辆) | 乙村(元/辆) | ||
| 大货车 | 70 | 800 | 900 |
| 小货车 | 35 | 400 | 600 |
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
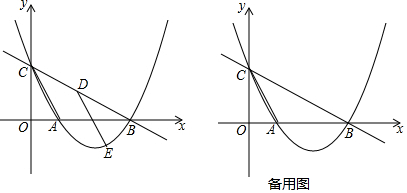
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com