
科目: 来源: 题型:解答题
| 重量(千克) 费用(元) | 0.5 | 1 | 3 | 4 | … |
| 甲公司 | 11 | 22 | 52 | 67 | … |
| 乙公司 | 11 | 19 | 51 | 67 | … |
查看答案和解析>>
科目: 来源: 题型:填空题
 三国时期吴国赵爽创造了“勾股圆方图”(如图)证明了勾股定理,在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的一个小正方形EFGH组成的,已知小正方形的边长是2,每个直角三角形的短直角边长是6,则大正方形ABCD的面积是100.
三国时期吴国赵爽创造了“勾股圆方图”(如图)证明了勾股定理,在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的一个小正方形EFGH组成的,已知小正方形的边长是2,每个直角三角形的短直角边长是6,则大正方形ABCD的面积是100.查看答案和解析>>
科目: 来源: 题型:填空题
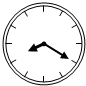 小明在他家里的时钟上安装了一个电脑软件,他设定当钟声在n点钟响起后,下一次则在(3n-1)小时后响起,例如钟声第一次在3点钟响起,那么第2次在(3×3-1=8)小时后,也就是11点响起,第3次在(3×11-1=32)小时后,即7点响起,以此类推…;现在第1次钟声响起时为2点钟,那么第3次响起时为3点,第2017次响起时为11点(如图钟表,时间为12小时制).
小明在他家里的时钟上安装了一个电脑软件,他设定当钟声在n点钟响起后,下一次则在(3n-1)小时后响起,例如钟声第一次在3点钟响起,那么第2次在(3×3-1=8)小时后,也就是11点响起,第3次在(3×11-1=32)小时后,即7点响起,以此类推…;现在第1次钟声响起时为2点钟,那么第3次响起时为3点,第2017次响起时为11点(如图钟表,时间为12小时制).查看答案和解析>>
科目: 来源: 题型:解答题
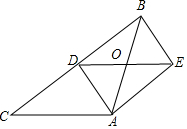 如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
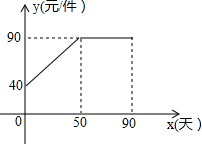 九年级(1)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售的相关信息如图,已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为W(单位:元).
九年级(1)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售的相关信息如图,已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为W(单位:元).| 时间x(天) | 1 | 30 | 60 | 90 |
| 每天销售量 p(件) | 198 | 140 | 80 | 20 |
查看答案和解析>>
科目: 来源: 题型:解答题
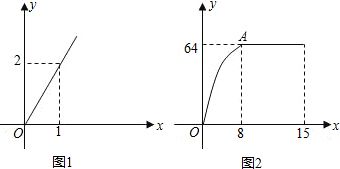
查看答案和解析>>
科目: 来源: 题型:解答题
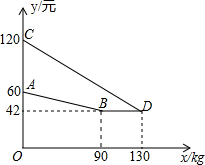 某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABCD、线段CD分别表示该产品每千克生产成本y1(单位:元)销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABCD、线段CD分别表示该产品每千克生产成本y1(单位:元)销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.查看答案和解析>>
科目: 来源: 题型:解答题
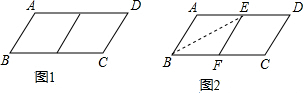 邻边不相等的平行四边形纸片,减去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,平行四边形ABCD中,若AB=1,BC=2,则平行四边形ABCD为1阶准菱形.
邻边不相等的平行四边形纸片,减去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,平行四边形ABCD中,若AB=1,BC=2,则平行四边形ABCD为1阶准菱形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com