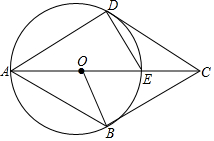18．已知，四边形ABCD中，E是对角线AC上一点，DE=EC，以AE为直径的⊙O与边CD相切于点D．B点在⊙O上，连接OB．
（1）求证：DE=OE；
（2）若CD∥AB，求证：四边形ABCD是菱形．

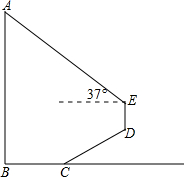17．如图，某数学活动小组为测量学校旗杆AB的高度，沿旗杆正前方2$\sqrt{3}$米处的点C出发，沿斜面坡度i=1：$\sqrt{3}$的斜坡CD前进4米到达点D，在点D处安置测角仪，测得旗杆顶部A的仰角为37°，量得仪器的高DE为1.5米．已知A、B、C、D、E在同一平面内，AB⊥BC，AB∥DE．求旗杆AB的高度．（参考数据：sin37°≈$\frac{3}{5}$，cos37°≈$\frac{4}{5}$，tan37°≈$\frac{3}{4}$．计算结果保留根号）

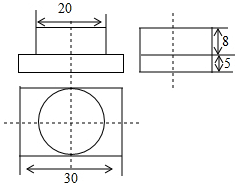16．如图是某几何体的三视图，根据图中的数据，求得该几何体的体积为（　　）

A．

800π+1200

B．

160π+1700

C．

3200π+1200

D．

800π+3000

15．如图1，△ABC是边长为4cm的等边三角形，边AB在射线OM上，且OA=6cm，点D从O点出发，沿OM的方向以1cm/s的速度运动，当D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连结DE．
（1）求证：△CDE是等边三角形；
（2）如图2，当6＜t＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE的最小周长；若不存在，请说明理由；
（3）如图3，当点D在射线OM上运动时，是否存在以D、E、B为顶点的三角形是直角三角形？若存在，求出此时t的值；若不存在，请说明理由．

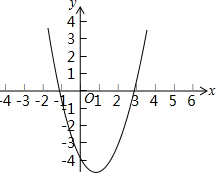14．设a、b是任意两个实数，用max{a，b}表示a、b两数中较大者，例如：max{-1，-1}=-1，max{1，2}=2，max{4，3}=4，参照上面的材料，解答下列问题：
（1）max{5，2}=5，max{0，3}=3；
（2）若max{3x+1，-x+1}=-x+1，求x的取值范围；
（3）求函数y=x²-2x-4与y=-x+2的图象的交点坐标，函数y=x²-2x-4的图象如图所示，请你在图中作出函数y=-x+2的图象，并根据图象直接写出max{-x+2，x²-2x-4}的最小值．

13．如图，AB是⊙O的弦，BC切⊙O于点B，AD⊥BC，垂足为D，OA是⊙O的半径，且OA=3．
（1）求证：AB平分∠OAD；
（2）若点E是优弧$\widehat{AEB}$上一点，且∠AEB=60°，求扇形OAB的面积．（计算结果保留π）

12．如图所示，C城市在A城市正东方向，现计划在A、C两城市间修建一条高速公路（即线段AC），经测量，森林保护区的中心P在A城市的北偏东60°方向上，在线段AC上距A城市120km的B处测得P在北偏东30°方向上，已知森林保护区是以点P为圆心，100km为半径的圆形区域，请问计划修建的这条高速公路是否穿越保护区，为什么？（参考数据：$\sqrt{3}$≈1.73）

11．某工厂有甲种原料130kg，乙种原料144kg．现用这两种原料生产出A，B两种产品共30件．已知生产每件A产品需甲种原料5kg，乙种原料4kg，且每件A产品可获利700元；生产每件B产品需甲种原料3kg，乙种原料6kg，且每件B产品可获利900元．设生产A产品x件（产品件数为整数件），根据以上信息解答下列问题：
（1）生产A，B两种产品的方案有哪几种；
（2）设生产这30件产品可获利y元，写出y关于x的函数解析式，写出（1）中利润最大的方案，并求出最大利润．

10．在平面直角坐标系xOy中，规定：抛物线y=a（x-h）²+k的伴随直线为y=a（x-h）+k．例如：抛物线y=2（x+1）²-3的伴随直线为y=2（x+1）-3，即y=2x-1．
（1）在上面规定下，抛物线y=（x+1）²-4的顶点坐标为（-1，-4），伴随直线为y=x-3，抛物线y=（x+1）²-4与其伴随直线的交点坐标为（0，-3）和（-1，-4）；
（2）如图，顶点在第一象限的抛物线y=m（x-1）²-4m与其伴随直线相交于点A，B（点A在点B的左侧），与x轴交于点C，D．
①若∠CAB=90°，求m的值；
②如果点P（x，y）是直线BC上方抛物线上的一个动点，△PBC的面积记为S，当S取得最大值$\frac{27}{4}$时，求m的值．

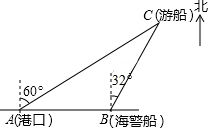9．（7分）一艘游船从港口A处以北偏东60°的方向出港观光．航行170海里至C处时发生了事故．船长立即发出了求救信号．一艘在港口正东方向B处的海警船接到求救信号，测得事故船在它的北偏东32°方向．若海警船以60海里/时的速度前往救援，求海警船到达事故船C处大约所需的时间．（精确到0.1小时）【参考数据：sin32°=0.53，cos32°=0.85．tan32°=0.62】