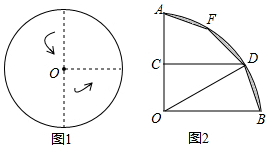16．如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB．已知OA=6，取OA的中点C，过点C作CD⊥OA交$\widehat{AB}$于点D，点F是$\widehat{AB}$上一点．若将扇形BOD沿OD翻折，点B恰好与点F重合，用剪刀沿着线段BD，DF，FA依次剪下，则剪下的纸片（形状同阴影图形）面积之和为36π-108．

15．如图是由5个全等的正方形拼成的图形，把它剪成一个大正方形，并使剪痕的条数最少．

14．设一元二次方程ax²+bx+c=0（a≠0）的两根为x₁，x₂，则据求根公式可得两根与方程系数之间有如下关系：x₁+x₂=-$\frac{b}{a}$，x₁•x₂=$\frac{c}{a}$．根据该结论求值：已知x₁，x₂是方程x²+6x+3=0的两实数根，则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值为（　　）

A．

2

B．

-2

C．

6

D．

-6

13．阅读下面材料：
小明遇到这样两个问题：

（1）如图1，AB是⊙O的直径，C是⊙O上一点，OD⊥AC，垂足为D，BC=-6，求OD的长；
（2）如图2△ABC中，AB=6，AC=4，点D为BC的中点，求AD的取值范围．
对于问题（1），小明发现根据垂径定理，可以得出点D是AC的中点，利用三角形中位线定理可以解决；对于问题（2），小明发现延长AD到E，使DE=AD，连接BE，可以得到全等三角形，通过计算可以解决．
请回答：
问题（1）中OD长为3；问题（2）中AD的取值范围是1＜AD＜5；
参考小明思考问题的方法，解决下面的问题：
（3）如图3，△ABC中，∠BAC=90°，点D、E分别在AB、AC上，BE与CD相交于点F，AC=mEC，AB=2$\sqrt{m}$EC，AD=nDB．
①当n=1时，如图4，在图中找出与CE相等的线段，并加以证明；
②直接写出$\frac{CE}{EF}$的值（用含m、n的代数式表示）．

12．已知关于x、y的方程组$\left\{\begin{array}{l}{x+y=1-a}\\{x-y=3a+5}\end{array}$，给出下列说法：
①当a=1时，方程组的解也是方程x+y=2的一个解；
②当x-2y＞8时，a＞$\frac{1}{5}$；
③不论a取什么实数，2x+y的值始终不变；
④若y=x²+5，则a=-4． 以上说法正确的是（　　）

A．

②③④

B．

①②④

C．

③④

D．

②③

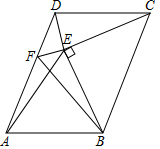11．如图，在?ABCD中，以BC为斜边在?ABCD内作等腰直角△BCE，连接DE，过点E作EF⊥DE交AD于点F，∠CDE=∠CED=∠DCB．
（1）若BC=2$\sqrt{2}$，求AE的长；
（2）连接FB，求证：EF+FA=FB．

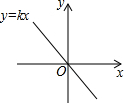10．已知函数y=kx的图象如图所示，则对一元二次方程x²+x+k-1=0根的情况，说法正确的是（　　）

	A．	没有实数根		B．	有两个相等的实数根
	C．	有两个不相等的实数根		D．	无法确定

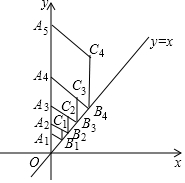9．如图，在平面直角坐标系中，点A₁的坐标为（0，1），过点A₁作直线y=x的垂线，垂足为点B₁，以A₁B₁为边作菱形A₁B₂C₂A₃，使得点A2落在y轴上，延长A₂C₁交直线于点B₂，再以A₂B₂为边作菱形A₂B₂C₂A₃，使得点A₃落在y轴上…按此作法继续作菱形，则点A₂₀₁₇的坐标是[0，（1+$\frac{\sqrt{2}}{2}$）²⁰¹⁶]．

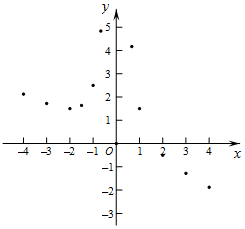8．有这样一个问题：探究函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质．
小东根据学习函数的经验，对函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质进行了探究．
下面是小东的探究过程，请补充完整，并解决相关问题：
（1）函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值，求m的值；

x

…

-4

-3

-2

-$\frac{3}{2}$

-1

-$\frac{2}{3}$

$\frac{2}{3}$

1

2

3

4

…

y

…

$\frac{17}{8}$

$\frac{31}{18}$

$\frac{3}{2}$

$\frac{59}{36}$

$\frac{5}{2}$

$\frac{29}{6}$

$\frac{25}{6}$

$\frac{3}{2}$

-$\frac{1}{2}$

-$\frac{23}{18}$

m

…

（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）进一步探究发现，该函数图象在第二象限内的最低点的坐标是（-2，$\frac{3}{2}$），结合函数的图象，写出该函数的其它性质（一条即可）当x＞0时，y随x的增大而减小．
（5）根据函数图象估算方程$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x=2的根为x₁=-3.8，x₂=-1.8．（精确到0.1）

7．解方程：
（1）$\frac{1}{x+3}$-$\frac{2}{3-x}$=$\frac{12}{{x}^{2}-9}$；
（2）$\frac{x}{x-1}$-$\frac{3}{{x}^{2}-1}$=1．