17．某校计划组织师生共300人参加一次大型公益活动，如果租用6辆大客车和5辆小客车恰好全部坐满．已知每辆大客车的乘客座位数比小客车多17个．
（1）求每辆大客车和每辆小客车的乘客座位数；
（2）由于最后参加活动的人数增加了30人，学校决定调整租车方案．在保持租用车辆总数不变的情况下，为将所有参加活动的师生装载完成，求租用小客车数量的最大值．

16．在面积都相等的所有矩形中，当其中一个矩形的一边长为1时，它的另一边长为3．
（1）设矩形的相邻两边长分别为x，y．
①求y关于x的函数表达式；
②当y≥3时，求x的取值范围；
（2）圆圆说其中有一个矩形的周长为6，方方说有一个矩形的周长为10，你认为圆圆和方方的说法对吗？为什么？

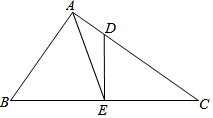15．如图，在Rt△ABC中，∠BAC=90°，AB=15，AC=20，点D在边AC上，AD=5，DE⊥BC于点E，连结AE，则△ABE的面积等于78．

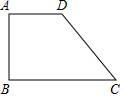14．如图，梯形ABCD中，∠ABC=∠BAD=90°，AD=AB=1，∠BCD=45°．将梯形ABCD折叠，使得点C与点A重合，折痕交CD于E，交BC于F，画出图形．求出折叠后重叠部分的面积．

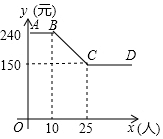13．某公司组织员工到附近的景点旅游，根据旅行社提供的收费方案，绘制了如图所示的图象，图中折线ABCD表示人均收费y（元）与参加旅游的人数x（人）之间的函数关系．
（1）当参加旅游的人数不超过10人时，人均收费为240元；
（2）如果该公司支付给旅行社3600元，那么参加这次旅游的人数是多少？

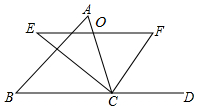12．如图，在△ABC中，点O是边AC上一个动点，过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F．
（1）若CE=8，CF=6，求OC的长；
（2）连接AE、AF．问：当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．

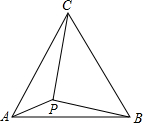11．如图，△ABC为等边三角形，AB=2．若P为△ABC内一动点，且满足∠PAB=∠ACP，则线段PB长度的最小值为$\frac{2\sqrt{3}}{3}$．

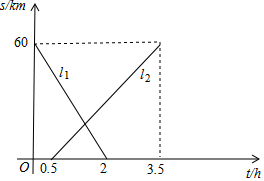10．A，B两地相距60km，甲、乙两人从两地出发相向而行，甲先出发．图中l₁，l₂表示两人离A地的距离s（km）与时间t（h）的关系，请结合图象解答下列问题：
（1）表示乙离A地的距离与时间关系的图象是l₂（填l₁或l₂）；
甲的速度是30km/h，乙的速度是20km/h；
（2）甲出发多少小时两人恰好相距5km？

9．已知单项式9a^m+1bⁿ⁺¹与-2a^2m-1b^2n-1的积与5a³b⁶是同类项，求mⁿ的值（　　）

A．

4

B．

3

C．

2

D．

1

8．观察下列等式：
第一个等式：${a}_{1}=\frac{2}{1+3×2+2×{2}^{2}}=\frac{1}{2+1}-\frac{1}{{2}^{2}+1}$
第二个等式：${a}_{2}=\frac{{2}^{2}}{1+3×{2}^{2}+2×（{2}^{2}）^{2}}=\frac{1}{{2}^{2}+1}-\frac{1}{{2}^{3}+1}$
第三个等式：${a}_{3}=\frac{{2}^{3}}{1+3×{2}^{3}+2×（{2}^{3}）^{2}}=\frac{1}{{2}^{3}+1}-\frac{1}{{2}^{4}+1}$
第四个等式：${a}_{4}=\frac{{2}^{4}}{1+3×{2}^{4}+2×（{2}^{4}）^{2}}=\frac{1}{{2}^{4}+1}-\frac{1}{{2}^{5}+1}$
按上述规律，回答下列问题：
（1）请写出第六个等式：a₆=$\frac{{2}^{6}}{1+3×{2}^{6}+2×（{2}^{6}）^{2}}$=$\frac{1}{{2}^{6}+1}$-$\frac{1}{{2}^{7}+1}$；
（2）用含n的代数式表示第n个等式：a_n=$\frac{{2}^{n}}{1+3×{2}^{n}+2×（{2}^{n}）^{2}}$=$\frac{1}{{2}^{n}+1}$-$\frac{1}{{2}^{n+1}+1}$；
（3）a₁+a₂+a₃+a₄+a₅+a₆=$\frac{14}{43}$（得出最简结果）；
（4）计算：a₁+a₂+…+a_n．