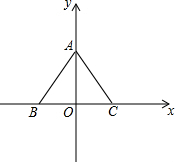14．如图，△ABC在平面直角坐标系中的位置如图所示，若S_△ABC=12，BC=2OC，且AC，BC的长满足$\left\{\begin{array}{l}{BC-AC=1}\\{BC+AC=11}\end{array}\right.$．
（1）求线段AC，BC的长；
（2）若E为x轴上一点，且S_△AOE=$\frac{16}{3}$，求点E的坐标；
（3）在x轴上是否存在一点P，使△ACP是以AC为腰的等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

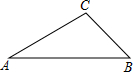13．已知：△ABC，AB=4，AC=3，以CB为边作等边三角形△CBP，连接AP，求AP的值．
这道题目难到了小明，首先没有图形，然后发现△ABC不是一个固定的图形，等边三角形△CBP也没有指定在BC所在直线的哪一侧，这两个不确定的因素会使得AP的值不一定是固定的长度，为此小明从特殊情况出发研究这个问题，按如下步骤进行了解决：
步骤1：取∠CAB=30°，以CB为边作等边三角形△CBP，使点A与点P在BC所在直线的异侧；
步骤2：要想建立AB，AC，AP的联系，需要将这三条线段进行转移处理，由于图中有等边三角形，可以通过旋转来完成线段与角的转移，因此将△ACP以P点为旋转中心，逆时针旋转60°，得到△P′BP，通过推理与计算得到了此位置时AP的值．
（1）请结合小明的步骤补全图形；
（2）结合补全后的图形求出AP的值；
（3）根据上述经验，改变∠CAB的度数，发现∠CAB在变化到某一角度时，AP有最大值，画出这个特殊角度时的示意图，写出AP的最大值，并说明取得最大值的思路．

12．2016年11月-2017年4月某省“共享单车”的用户使用情况如图，根据统计表中提供的信息，预估2017年5月该省共享单车的使用用户约3400万人，你的预估理由是与3-4月份增幅持平．

11．方程2x²+1=3x的两个根为（　　）

A．

x1=2，x2=1

B．

x1=$\frac{1}{2}$，x2=1

C．

x1=-2，x2=1

D．

x1=-$\frac{1}{2}$，x2=1

10．在我市创建“文明城市”的工作中，社区计划对某区域进行绿化，经投标，由甲、乙两个施工队来完成，已知甲队每天能完成的绿化面积是乙队每天能完成的绿化面积的2倍，并且在独立完成面积为300m²区域的绿化时，甲队比乙队少用3天，求甲、乙两施工队每天分别能完成xm²的绿化面积，则可列方程为$\frac{300}{2x}$+3=$\frac{300}{x}$．

9．解方程：3x（x+4）=2x（x+5）+8．

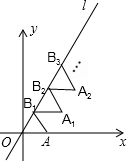8．如图，等边三角形△OAB₁的一边OA在x轴上，且OA=1，当△OAB₁沿直线l滚动，使一边与直线l重合得到△B₁A₁B₂，△B₂A₂B₃，…则点A₂₀₁₇的坐标是（$\frac{2019}{2}$，$\frac{2017\sqrt{3}}{2}$）．

7．如图1，在△ABC中，点D为边AC上一点，且∠DBC=∠BAC．
（1）求证：BC²=CD•AC；
（2）如图2，点E、G分别是BC，DC边上一点，连接AE交BD于点F，连接EG，且∠BDC+∠AEG=180°，
①若点E为BC中点，$\frac{EG}{EF}=\frac{1}{\sqrt{5}}$，求$\frac{AB}{BC}$的值；
②若$\frac{BE}{CE}=\frac{1}{n}$，$\frac{EG}{EF}=\frac{1}{k}$，求$\frac{AB}{BC}$的值（用含n，k的式子表示）

6．明朝的数学家程大位在《算法统宗》中有一道古诗趣题：甲赶群羊逐草茂，乙拽只羊随其后，戏问甲及一百否？甲云所曰无差谬；若得这般一群羊，再添半群小半群，得你一只来方凑，玄机妙算谁猜透？其大意是：甲赶一群羊去放，乙也牵着一只羊跟在甲的后面．乙问甲：“你的这群羊有没有一百只呢？”甲说：“我再得这样的一群羊，再得这群羊的一半，还得这群羊的四分之一，最后凑上你的这只羊，正好是一百只．”问甲原有多少只羊？设甲原有x只羊，根据题意，可列方程为x+x+$\frac{1}{2}$x+$\frac{1}{4}$x+1=100．

5．①$\sqrt{\frac{1}{16}}$-$\sqrt{6\frac{1}{4}}$+|$\sqrt{3}$-π|+$\sqrt{3}$．
②已知$\sqrt{25}$=x，$\sqrt{y}$=2，z是9的平方根，求2x+y-5z的值．
③3（x+1）²=48，求x．
④已知点P（m+3，m+1）在直角坐标系的坐标轴上，求m的值与点P的坐标．
⑤用适当的方法解下列方程组：$\left\{\begin{array}{l}x+5=3（y+1）\\ 5（x-1）=3（y+5）\end{array}$．