科目： 来源： 题型：选择题

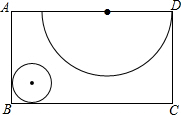20．如图，矩形ABCD纸板中，剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型，若已知小圆的半径为1cm，则此圆锥的全面积是（　　）

A．

2πcm

B．

3πcm

C．

$\sqrt{3}$πcm

D．

（$\sqrt{3}$+1）πcm

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

18．某兴趣小组在研究用一副三角板拼角时，小明，小亮分别拼出了图1，图2所示的两种图形，小明把30°和90°的角按如图1方式拼在一起；小亮把30°和90°的角按如图2方式拼在一起，并在各自所拼的图形中分别作出∠AOB、∠COD的平分线OE、OF．

（1）请你计算出图1中∠EOF的度数；
（2）仿照图1的求解方法，计算图2中∠EOF的度数；
归纳 若有公共定点的两个角∠α，∠β（∠α＞∠β）有一条边重合，请你直接写出这两个角的平分线所夹的角的度数．（α、β的代数式表示）

科目： 来源： 题型：解答题

科目： 来源： 题型：选择题

科目： 来源： 题型：填空题

15．如图所示，一水库迎水坡AB的坡度i=1：2，则求坡角α的正弦值sinα=$\frac{\sqrt{5}}{5}$．

科目： 来源： 题型：选择题

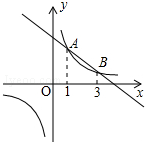14．如图，在平面直角坐标系中，反比例函数y₁=$\frac{3}{x}$的图象与一次函数y₂=kx+b的图象交于A、B两点．若y₁＜y₂，则x的取值范围是（　　）

A．

1＜x＜3

B．

x＜0或1＜x＜3

C．

0＜x＜1

D．

x＞3或0＜x＜1

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

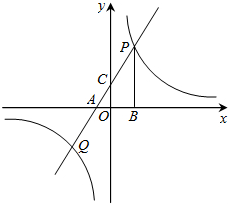12．如图，经过点A（-2，0）的一次函数y=ax+b（a≠0）与反比例函数y=$\frac{k}{x}$（k≠0）的图象相交于P、Q两点，过点P作PB⊥x轴于点B．已知tan∠PAB=$\frac{3}{2}$，点B的坐标为（4，0）．
（1）求反比例函数和一次函数的解析式；
（2）连接BQ，求△PBQ的面积．

科目： 来源： 题型：解答题